Площадь поверхности тела вращения равна:
площади двух конусов с радиусом основания - высотой треугольника из вершины основания к боковой стороне и образующими:
большей, равной боковой стороне данного треугольника, и
меньшей, равной его основанию.
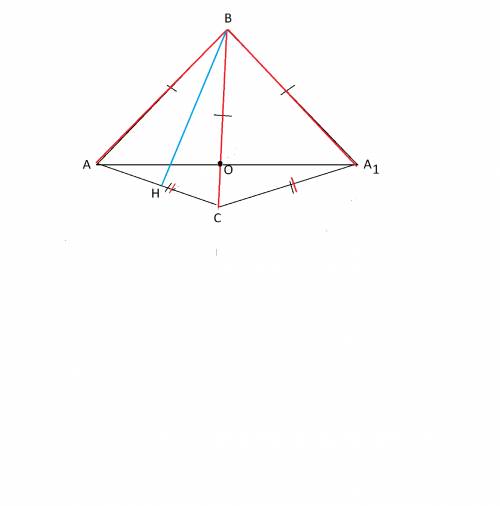
Запишем это в виде выражения - согласно приложенному рисунку.
S₁ бок конуса₁= πrl₁
S₂ бок конуса₂= πrl₂
S₁+S₂=πrl₁+πrl₂=πr(l₁+l₂)
r=AO
l₁=АВ
l₂=АС
S АВА₁С= πАО(АВ+АС)
Из нужных для решения величин имеем
длину АС =6- основания треугольника, и
его высоты ВН=. 6√2
Необходимо найти образующую АВ - боковоую сторону треугольника,
и радиус АО - высоту треугольника к боковой стороне.
АО=2 S АВС:ВС.
ВС=АС=√(ВН²+АН²)=√(72+9)=9
2 S АВС=ВН·АС =6·6√2=36√2
АО=2*(18√2):9=4√2
Подставим найденное в S АВА₁С =πАО(АВ+АС)
S АВА₁С= π4√2(9+6)=60π√2
диагональ делит острый угол (угол А, и т. к. трап. равнобедр. и угол С), то Угол ВАС = углу САД = углу ВСА = углу ДСА из этого выходит: что треугольник ВСА равнобедренный, то есть АВ = ВС = 15см. Проведем высоту ВК и высоту СО, образуем прямоугольник ВКОС, по свойствам прямоугольника ВС=КД, тость по 15см. ЧТобы найти АК и ОД (которые равно. трапеция равносторонняя) (33-15):2=9см.
По теореме пифагора найдем (в треугольнике АВК) катет ВК(высоту): (на клаве нет корня и квадрата, поэтому реши сам(сама) получится: 12см.. площадь трапеции = произведению полсумы основ на высоту, то: ((ВС+АД):2)и все это умножить на ВК (высоту)= ((15+33):2)*12
Для этого опустим в трапеции АВСН высоты
Таким образом стороны прямоугольника равны АВ и