1)Угол BAC делится биссектрисой AD пополам => Угол DAC=40градусов
2)Т.к. треугольник равнобедренный, то Угол DCA также будет =40градусов
3)Угол ADC=180-40-40=100градусов
Вывод:
Угол DAC= Угол DCA= 40градусов
Угол ADC= 100градусов
ответ: АР=8
Объяснение (подробно):
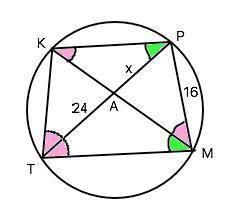
ТР - биссектриса ⇒ ∠КТР=∠РТМ.
Т.к. около четырехугольника описана окружность, все углы, вершины которых лежат на ней, -вписанные. Вписанные углы, которые опираются на одну дугу, равны; равны и хорды, которые стягивают равные дуги.
Угол РМК опирается на дугу РК, и угол КТР опираются на дугу КР, следовательно они равны. Но им равен и угол РТМ , следовательно, равны хорды КР=РМ=16.
Примем АР=х. Тогда ТР=ТА+х=24+х
Рассмотрим ∆ ТКР и АКР. Они имеют по два равных угла, следовательно, подобны. Из их подобия следует отношение ТР:КР=КР:АР ⇒
(24+х):16=16:х
Из пропорции получаем 14х+х²=256 ⇒ х²+24х-256. Решив квадратное уравнение находим х₁=8; х₂=-32 ( не подходит).
АР=х=8.
а где продолжение условия? основанием пирамиды dabc является правильный треугольник abc сторона которого = ребро da перпендикулярно к плоскости авс , а плоскость dbc составляет с плоскостью авс угол 30*. найдите площадь боковой поверхности пирамиды. условие такое? если такое, то вот решение : s(бок) = 2s(адс) + s(всд) угол дка = 30, тогда ад = ак* tg30 = (av3/2)*v3/3 =a/2 тогда s(асд) = 1/2*а*а/2 = а^2 / 4 дк = а, тогда s(всд) = 1/2*а*а = а^2 / 2 s(бок) = 2*(а^2 / 4) * (а^2 / 2) = а^2