
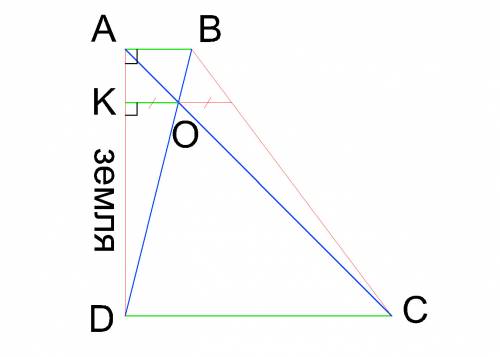
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
1. Если две противоположные стороны четырехугольника равны и параллельны, то такой четырехугольник параллелограмм.
2. Сумма углов параллелограмма , прилежащих к одной стороне , равна 180 градусов.
3. Верно ли следующее высказывание :
а) Диагонали параллелограмма делят его на четыре равных треугольника. - нет
б) Четырехугольник у которого две стороны параллельны и равны , называется параллелограммом. - да
в) Может ли один угол параллелограмма быть равным 30º, а другой - 50º? - нет, потому что сумма углов, прилежащих к одной стороне, 180 градусов
4. Четырехугольник АВСД – параллелограмм. Если ∟В = 70º, то угол Д =70 градусов, т.к. противолежащие углы параллелограмма равны
Сумма двух соседних сторон параллелограмма равна 10 см. Чему равен его периметр? - Р=10*2=20 см.