Будем считать, что задание дано так:
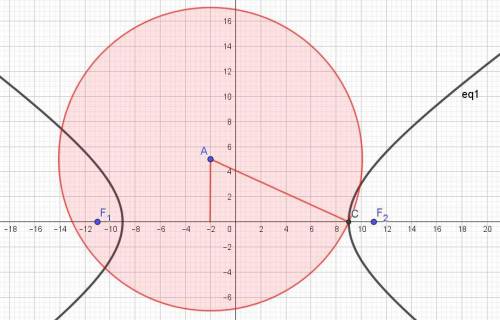
Определить уравнение окружности, проходящей через правую вершину гиперболы 40x² - 81y² = 3240 и имеющей центр в точке А(-2; 5).
Уравнение гиперболы приведём к каноническому виду, разделив обе части заданного уравнения на 3240:
(x²/81) - (y²/40) = 1.
Или так: (x²/9²) - (y²/(2√10)²) = 1 это и есть каноническое уравнение.
Отсюда находим координаты правой вершины гиперболы: С(9; 0).
Теперь находим радиус заданной окружности как отрезок АС.
АС = √((9 - (-2))² + (0 - 5)²) = √(121 + 25) = √146.
Получаем ответ: (x + 2)² + (y - 5)² = 146.
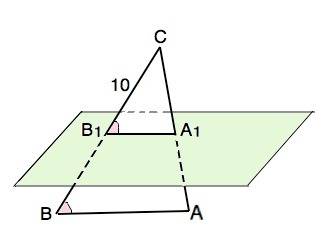
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
Т.е. 13²=12²+х²
Отсюда х²=13²-12²
Отсюда х=√13²-12²
х=√169-144
х=√25
х=5
Значит,второй катет прямоугольного треугольника равен 5 см.
ответ: катет 5 см,гипотенуза 13 см.
Удачи!