Question

Втреугольнике abc угол c прямой, ab=2 см, угол b=60 градусов, mc перпендикулярен (abc), mc=2 см. найдите площадь треугольника amb. напишите решение поподробнее

Answer 1

ΔABC   прямоугольный, ∠С = 90°, ∠B = 60°, AB = 2 см

CH ⊥ AB   - высота треугольника  ABC

$BC = AB\cdot \cos 60^o=2\cdot \dfrac 12=1 \\\\ AC=AB\cdot \sin 60^o=2\cdot \dfrac {\sqrt3}2=\sqrt3 \\\\ CH=\dfrac{BC\cdot AC}{AB}=\dfrac{1\cdot \sqrt3}{2}=\dfrac{\sqrt3}{2}$

МС ⊥ (ABC)  ⇒  MC  перпендикулярна  любой прямой, лежащей в плоскости треугольника ABC  ⇒   MC ⊥ CH

MC ⊥ CH,  CH ⊥ AB   ⇒    MH ⊥ AB   -  по теореме о трёх перпендикулярах.

ΔMCH  - прямоугольный,  ∠MCH = 90°, MC = 2 см,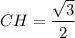  $CH=\dfrac{\sqrt3}2$ см.   По теореме Пифагора

$MH^2=MC^2+CH^2=2^2+\Big(\dfrac{\sqrt3}2\Big)^2=4+\dfrac 34=\dfrac{19}4 \\ \\ MH=\sqrt{\dfrac{19}4}=\dfrac{\sqrt{19}}2 \\ \\ S_{AMB}=\dfrac 12\cdot AB\cdot MH=\dfrac 12\cdot 2\cdot \dfrac{\sqrt{19}}2=0,5\sqrt{19}$

ответ:  0,5√19 см²