2-й катет выражается следующим образом:
по определению тангенса, как отношения противолежащей стороны к прилежащей
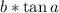
Прилежащий к нему угол будет равен по теореме о сумме углов в треугольнике (равна 180 градусам). Один из углов прямой, другой равен а. Тогда
180-90-а=90-а
Квадрат гипотенузы равен по теореме Пифагора (можно и легче)
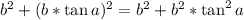
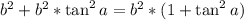
По известному тождеству
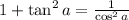
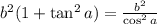
То есть сама гипотенуза равна
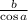
Подставим
Согласно условию b=12 см , а = 35, 2-й катет равен
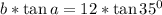
Другой угол равен
90-35=55 - градусов
Гипотенуза равна
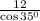
Пусть коэффициент отношений диагоналей равен x.
Тогда короткая диагональ будет 2х, а длинная 7х.
Половина каждой из них будет х и 3,5х соответственно.
Из прямоугольного треугольника с гипотенузой, равное стороне ромба 53:4=13,25 и катетами х и 3,5х, равными половинами диагоналей, найдем по т.Пифагора величину х.
x^2+(3,5х)^2=(13,25)^2
13,25x^2=(13,25)^2
x^2=13,25
x=корень из 13,25
2х=2*корень из 13,25
7х=7*корень из 13,25
Площадь ромба равна половине произведения его диагоналей.
S=7*корень из 13,25*2*корень из 13,25 = 92,75
Высоту ромба найдем по формуле:
S=h*a
S=h*13,25
h=92,75:13,25 = 7
ответ: 7.
Обозначим <1 = 1, <2 = 4, тогда сумма углов = 1 + 4 = 5 - односторон <
<1 = 180 : 5 = 36
< 2 = 36 * 4 = 144