Объяснение: (V -корень, ^ -знак степени, 3^2 -это 3 в квадрате)
находим все по теор. Пифагора
1) тр. ADC AD=V(4^2 +1^2)=V(17)
2) тр. DBC CB=V((V10)^2 - 1^2))=V9=3
3) тр. ACB AB=V(4^2+3^2)=V(16+9)=5
4) Медиана, проведенная к гипотенузе равна 1/2 гипотенузы, CM=1/2 AB,
CM=5/2
5) тр. DCM DM=V(1^2 +(5/2)^2)=V(29/4)=V(29) /2
6) проведем BK перпендикулярно МС и BK перпендикулярна DC, значит BK перпендикулярна плоскости DCM, значит, BK есть расстояние от точки B до плоскости DCM. Надо найти BK/
S(ABC)=1/2 AC*CB=1/2*4*3=6, тогда S(MCB)=6/2=3 и S(MCB)=1/2*MC*BK,
3=1/2*5/2 *BK, 12=5BK, BK=12/5=2,4 , расстояние =2,4
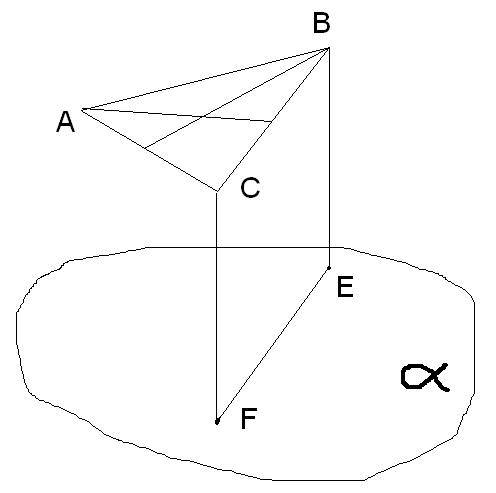
Поскольку в данном случае треугольник - фигура плоская, то все его медианы лежат в плоскости треугольника. И если две медианы параллельны плоскости альфа, то и треугольник параллелен этой плоскости. Таким образом, прямая ВС параллельна плоскости альфа. Поскольку прямые, проведенные из В и С параллельны между собой, то расстояние между точками Е и F на плоскости альфа будет равно расстоянию между В и С в плоскости треугольника. А так как плоскость треугольника параллельна плоскости альфа, то ВС будет параллельна ЕF. Длины параллельных прямых проведенных из В и С будут равны между собой, поскольку они проходят между двумя параллельными плоскостями (плоскостью альфа и плоскостью треугольника) Мы получили, что в четырехугольнике противоположные стороны попарно равны и параллельны. Значит этот четырехугольник параллелограмм.
Решим методом площадей. Площадь трапеции с одной стороны равна произведению полусуммы оснований на высоту трапеции, а с другой половине произведения диагоналей трапеции на синус ула между ними.
1) высоту трапеции примем за h. По первой формуле: S=0,5(10+12)h=11h
2) диагонали равнобокой трапеции равны, а синус прямого угла равен 1. По второй формуле: S=0,5*d1*d2=0,5*(d^2)/ Выразим d^2 по теореме Пифагора из прямоугольного тр-ка, образованного высотой h, диагональю d и частью нижнего основания, длина которой равна 10+(12-10)/2=10+1=11 (см). Итак, d^2=h^2+11^2. Тогда S=0,5*d^2=0,5(h^2+121).
3) Приравняем: 11h=0,5(h^2+121); => 22h=h^2+121; => h^2-22h+121=0; => (h-11)^2=0;
=> h-11=0; => h=11 (см)