Точка М лежит внутри двугранного угла величиной 120 градусов и удалена от его граней на расстояния соответственно 4 и 6. Найдите расстояние от М до ребра двугранного угла.
Опишу подробно.
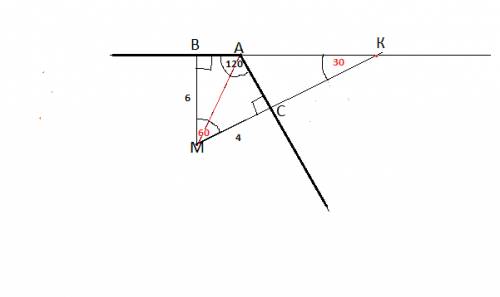
Рисуем данный угол 120° как бы в разрезе, т.е. вид сверху.
Обозначим вершину данного угла А.
В нутри угла отмечаем точку М.
Расстояние от точки до плоскости - перпендикуляр.
Опустим из М перпендикуляры к сторонам угла.
Обозначим точку пересечения со стороной угла более длинного отрезка, равного 6, - В , более короткого, равного 4, - С.
Т.к. сумма углов четырехугольника 360°, углы В и С прямые по построению, то
угол ВМС=180°-120°=60°.
Продлим сторону ВА и построим смежный с углом А угол.
Он, как смежный, равен 180°-120°=60°
Продлим МС до пересечения с ВА, обозначим точку пересечения К.
Получился прямоугольный треугольник ВМК.
В нем
угол ВМК равен 60° . угол ВКМ=30°
МК=ВМ:sin( 30°)=12
СК=МК-МС=12-4=8
АС=CК:Ctg (30°)=8:√3
Из прямоугольного треугольника АМС по теореме Пифагора найдем МА.
МА²=АС²+МС²=(8:√3)²+4²=64/3+16=112/3
МА=√(112/3)=4√(7/3)
т.к. угол А =90 градусов, а угол НАЕ=30 градусам, то, угол НАВ= 60 градусам, следовательно, угол В = 30 градусам.
Т.к. АЕ - это катет, лежащий напротив угла 30 градусов (напротив угла В), то катет равен 1/2 гипотенузы , те. 1/2 ВЕ.
Следовательно, ВЕ равно 2АЕ= 2*12=24
ВН/НА=НА/НЕ
НЕ= 6 ( лежит напротив угла 30градусов)
АН = sqrt (12^2-6^2)= sqrt108 (по т. Пифагора)
НА^2= ВН*НЕ=ВН*6
108=ВН*6
ВН=18, ВЕ=ВН+ЕН=18+6=24
b²-а²=D*d*cos α
где b и а- большая и меньшая стороны, D и d - большая и меньшая диагонали, α - угол между диагоналями.
Подставим известные величины:
36-16= D*d*cos 45º
D*d*cos45º =20
Одна из формул площади параллелограмма S=Dd* sinα:2
Синус и косинус 45º равны⇒
D*d*sin45º =20
S =Dd* sin45º:2=20:2=10(ед. площади)
---------
Данная выше формула выводится из т.косинусов.
-------
Обозначим для удобства большую сторону ВС параллелограмма b, меньшую СD- а, угол COD-α
Рассмотрим треугольник ВОС
Угол ВОС тупой и его косинус отрицательный.
По т.косинусов из ∆ ВОС
ВС²==ВО²+СО² -2ВО*СО*(-cosα)
b²= (d/2)²+(D/2)² + 2(d/2)*D/2*cos α
Из треугольника СОD по т.косинусов
а²=(d/2)²+(D/2)² - 2(d/2)*D/2*cos α
Вычтем из первого уравнения второе:
b²-а²= (d/2)²+(D/2)² + 2(d/2)*D/2*cos α - (d/2)² - (D/2)² + 2(d/2)*D/2*cos α
b²-а²= 4(d/2)*D/2*cosα=4Dd/4)*cos α
b²-а²=D*d*cos α