В современных человеческих популяциях уровень полученного образования обладает высокой наследуемостью, то есть сильно зависит от генов. Выявлены десятки аллелей, влияющих на этот признак. При этом образование, как правило, отрицательно коррелирует с дарвиновской при образованные люди хуже размножаются. Это указывает на возможный отбор против «генов образования». Новое исследование, основанное на данных по 110 000 исландцев, родившихся между 1910 и 1975 годами, показало, что «гены образования» действительно подвергаются отрицательному отбору. Эти аллели, многие из которых коррелируют также с повышенным интеллектом, крепким здоровьем и долгой жизнью, снижают при независимо от того, реализовал ли человек обусловленную ими склонность к получению хорошего образования. Исследование подтвердило опасения о том, что эволюция современного человечества направлена в сторону ухудшения генетического базиса признаков, связанных с интеллектом. Социально-культурное развитие пока с лихвой компенсирует генетическую деградацию, но со временем ее последствия могут стать существенными.
Объяснение:
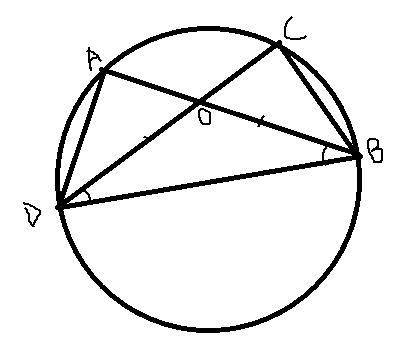
Дано: Хорды AB=CD пересекаются в точке О. Доказать: AO=CO, DO=BO.
Док-во: Соединим точки A B C D как на рисунке и рассмотрим треугольники ABD и CDB. Равные хорды стягивают равные дуги, значит вписанные углы ADB и CBD равны, а вписанные углы DAB и BCD опираются на одну и ту же дугу, значит они равны. Поскольку в треугольнике сумма углов равна 180°, то и оставшиеся углы ABD и CDB равны. Из равенства этих двух углов (<ABD=<CDB) следует, что △DOB - равнобедренный. => DO=BO. Поскольку AB=AO+BO и CD=DO+CO, а AB=CD, то и AO=CO, чтд.
По теореме о сумме углов треугольника, получим, что ∠ЕСА=∠ЕАС=(180-120)÷2=30°. (Равенство углов из св-ву равноб. треугольника).
Рассмотрим ΔАСВ: СЕ - биссектриса ∠С, а АЕ - биссектриса ∠А. По опр. биссектр.: ∠САЕ=∠ЕАВ=30, и ∠АСЕ=∠ВСЕ=30⇒∠С=60° и ∠А=60°⇒∠А=∠С⇒ΔАВС - равнобедренный(по св-ву).
По теореме о сумме углов треугольника, найдем ∠В: ∠В=180-60-60=60°⇒ ΔАВС - равносторонний(по св-ву)
Исходя из того, что внешние углы равны сумме не смежных с ними углов, а углы ΔАСВ равны, сделаем вывод, что внешние углы равны.
Найдем один из таковых: 60+60=120°
ответ: 120°(любой из внешних углов)