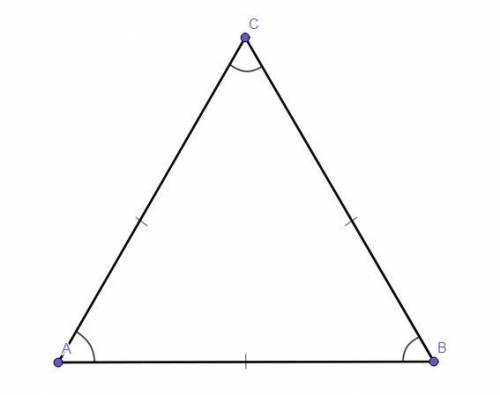
ΔАВС - равносторонний.
Доказать :∠А = ∠В = ∠С.
Доказательство :По определению равностороннего треугольника -
АВ = ВС = АС.
по свойству равнобедренного треугольника).Так как АВ = ВС, то ΔАВС - равнобедренный.
Углы у основания равнобедренного треугольника равны.Следовательно -
∠С = ∠А.
Но также АВ = АС.
Поэтому -
∠С = ∠В.
Теперь рассмотрим данное соотношение -
∠С = ∠А
∠С = ∠В
Отсюда следует, что -
∠А = ∠В = ∠С.
по соотношениям между сторонами и углами в треугольнике).Чем больше/меньше сторона в одном треугольнике, тем больше/меньше противолежащий угол в этом треугольнике.Не сложно догадаться, что -
Если в одном треугольнике равны стороны, то напротив этих сторон лежат равные углы.Так как -
АВ = ВС = АС
То и -
∠А = ∠В = ∠С.
- - -Что требовалось доказать!
d=4-4=0
x=2:2=1
tgx=1
x=p:4 + pk, k принадлежит Z