Рисунок прилагается
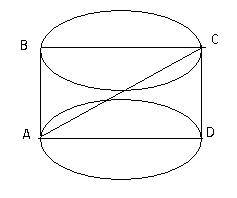
ABCD - нужное сечение
AC = 13см
Т.к. это цилиндр, осевое сечение явл. прямоугольником.
Обозн высоту h, а радиус r; r>h
Sсеч = h*2r
2rh = 60
Из треугольника ACD:
AC^2 = AD^2 + CD^2
169 = 4r^2 + h^2
Получается система:
4r^2 + h^2 = 169
2rh = 60
4r^2 + h^2 = 169
h = 30/r
Из 2 уравнения подставляем значение h в первое
4r^2 + 900/r^2 = 169
домножим на r^2
4r^4 + 900 - 169r^2 = 0
4r^4 - 169r^2 + 900 = 0
r^2 обозн. t
4t^2 - 169t + 900 = 0
D = 28561 - 14400 = 14161 = 119^2
t = (169 +- 119)/8 = 36 или 6,25
t = 36 или t = 6,25
r^2 = 36 или r^2 = 6,25
r = 6 или r = 2,5 (есть варианты и с минусами, но радиус и высота не могут быть отрицательными)
Значения r подставляем в одно из уравнений системы, чтобы найти h. При этом не забываем, что h<r
h = 30/r
r = 6
h = 5
6>5; r>h
удовл.
r = 2,5
h = 12
2,5<12;r<h
не удовл.
Значит r = 6; h = 5
Площадь полной поверхности:
Sполн = Sосн + Sбок = п*r^2 + 2п*r*h = п*6^2 + 2п*6*5 = 36п + 60п = 96п см^2
Объем:
V = Sосн*h = п*r^2*h = п*36*5 = 180п см^3
ответ: 96п см^2 и 180п см^3
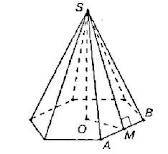
S осн = 6*а^2*корень из 3/4.
Видим, что надо знать сторону основания :а-?
3)S бок = 6*0,5* а*h, где h- апофема .Таким образом, от цели нас отделяет только нахождение стороны основания а. Из тр-ка МОS-прям.: SO = 12, SM =15, тогда ОМ=9 ( либо по теореме Пифагора, либо этот тр-к подобен "египетскому" с коэфф 3).
4)Из тр-ка АОМ-прям: ОМ =9 ,угол ОАМ =60 град., тогда АМ =9/корень из 3 = 3*корень из 3, тогда а = 2*АМ = 6*корень из 3.
5)Sполн = 6* (6*корень из 3)^2 *корень из 3/4+ 3* 6*корень из 3*15 =
= 6*36*3* *корень из 3/4 + 18*15* корень из 3= 6*9*3* *корень из 3 + 18*15* корень из 3 = 18*24* корень из 3 = 432* корень из 3 (кв.ед).