1) <А+<В=180°(св-во парал.)
<А=х°, тогда <В=х°+30°.
х°+х°+30°=180°
2х°=150°
х=75°
Тогда <А=75°, <В=75°+30°=105°.
ответ: <А=<С=75°, <В=<D=105°.
2) <А+<В=180°(св-во парал.)
<А=х, тогда <В=3х.
х+3х=180°
4х=180°
х=180°:4
х=45°
Тогда <А=45°, <В=45°*3=135°.
ответ: <А=<С=45°, <В=D=135°.
3) Если один из углов параллелограмма равен 90°, то такой параллелограмм - прямоугольник. Значит, все углы по 90°.
4) Если в параллелограмме диагонали равны, то такой параллелограмм - прямоугольник. Значит, все углы по 90°.
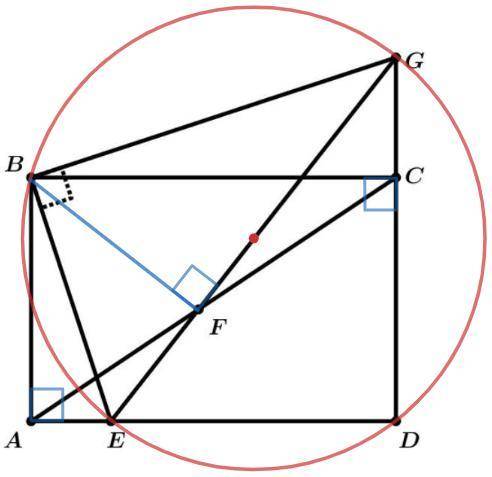
Точки A-F-C лежат на прямой Симсона точки B относительно треугольника EGD.
Объяснение:
Основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на прямой Симсона.
Точка B лежит на описанной окружности треугольника EGD (прямые углы EBG и EDG опираются на диаметр EG).
A и С - основания перпендикуляров из точки B на стороны треугольника EGD.
Тогда AC - прямая Симсона точки B относительно треугольника EGD.
(Прямая Симсона пересекает сторону EG в точке F, следовательно BF⊥EG)