Задача на подобие треугольников.
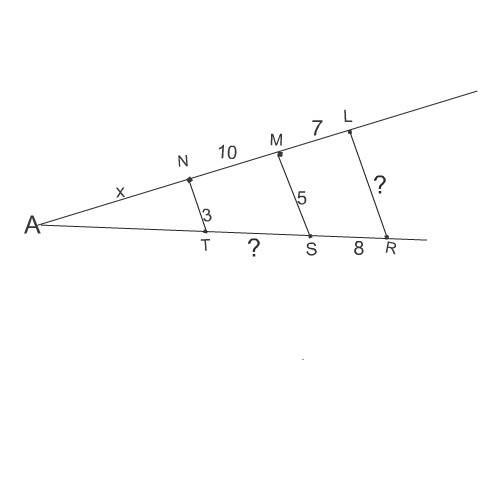
Обозначим вершину угла А.
Рассмотрим подобные треугольники AМS и ANT
Примем АN=x
x:(10+x)=3:5
5x=30+3x
2x=30
x=15
--------------------
Рассматриваем треугольники АМS и ALR
AL:AN=LR:NT
32:15=y:3
15y=96
y=6,4
LR=6,4
-------------------
Рассматриваем треугольники ASM ARL
Примем АS=z
Тогда
((z+8):z=6,4:5
5z+40=6,4z
1,4z=40
z=400/14=28 и 4/7
---------------------
И последнее. Рассмотрим треугольник АТN и AMS
AS:(AS-q)=5:3
(400/14):(400/14-q)=5:3
2000/14-5q=1200/14
5q=800/14
q=160/14=11 и 3/7
TS=11 ³/₇
---------------
Очень громоздкие вычисления, возможно, одна из данных в задаче величин должна быть иной.
я так думаю здесь нужно найти уравнение прямого, проходящего через центров данных кругов.
x²+y²-4x+2y=0 x²+y²-10x-6y=0
x²-2*2*x+4+y²+2*1*y+1-5=0 x²-2*5*x+25+y²-2*3*y+9-34=0
(x-2)²+(y+1)²=5 (x-5)²+(y-3)²=34
Centr O₁ (2;-1) Centr O₂ (5;3)
uravnenie pr9mogo
(x-2)/(5-2) = (y-(-1))/(3-(-1))
(x-2)/3 = (y+1)/4
4*(x-2) = 3*(y+1)
4x-8 = 3y+3
3y-4x+3+8=0
3y-4x+11=0