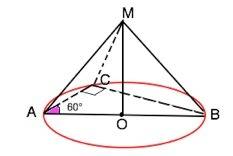
Обозначим пирамиду МАВС, МО - высота, угол С=90°, угол САВ=60°, ВС=4√3.
а) Вокруг основания треугольной пирамиды можно описать окружность. Так как все ребра пирамиды наклонены к плоскости основания под равным углом, их проекции равны радиусу описанной окружности, и основание высоты пирамиды - центр описанной окружности.
Центр окружности, описанной вокруг прямоугольного треугольника - середина гипотенузы, ч.т.д.
б) Боковые ребра данной пирамиды - наклонные с равными проекциями, следовательно они равны гипотенузам равнобедренных треугольников с катетами МО - высота пирамиды, и ВО=АО=СО - радиус описанной окружности основания.
АВ=АС:sin60°
АВ=4√3:(√3/2)=8
OB=8:2=4
MB=MA=MC=OB:sin45°=4:√2/2=4√2 (ед. длины)
1) h=2r S=(a+b)/2*h=4*4=16(см^2) если равнобедренная,то боковые стороны равны корню из (1+16)= корню из 17 P=2 корня из 17 + 8
2)средняя линия = 0.5(a+b) s=10*8=80(см^2)