PD-перпендикуляр, проведённый из точки P к плоскости (ABC); D-основание перпендикуляра; PB-наклонная; B-основание наклонной.
Значит DB-проекция наклонной на плоскость.
Но DB перпендикулярна AC(т.к. в квадрате диагонали перпендикулярны)
Проведём прямую а параллельную AC через основание наклонной(через В).
По лемме о перпендикулярности прямых(если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой): DB перпендикулярна a
По теореме о трёх перпендикулярах(прямая(a), проведенная в пплоскости через основание наклонной(B) перпендикулярно к ее проекции(DB) на эту плоскость, перпендикулярна и к самой наклонной(PB)):PB перпендикулярна a.
И опять по лемме о перпендикулярности прямых:a||AC, a перпендикулярна PB, значит AC перпендикулярна PB.
(что неясно-пиши в личку)

В соответствии с классическим определением, угол между векторами, отложенными от одной точки, определяется как кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. Для заданного варианта углы между векторами могут быть определены из соотношения углов в треугольнике ABC, в котором ∠АСВ=90°, ∠СВА=40°, соответственно ∠САВ=180°-(90°+40°)=50°. Тогда -
- угол между векторами СА и СВ равен ∠АСВ=90°;
- угол между векторами ВА и СА равен ∠САВ=50°;
- угол между векторами СВ и ВА равен ∠САВ+∠АСВ=50°+90°=140°
О нас
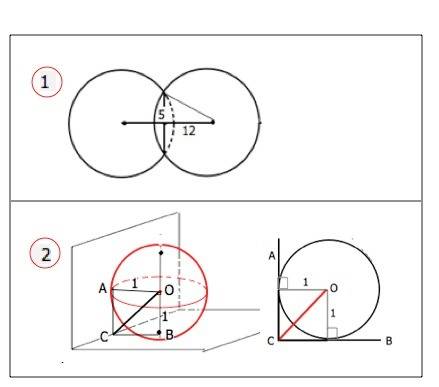
1) Рассмотрим сечение, проходящее через центры сфер.
Отрезок, соединяющий центры, перпендикулярен диаметру сечения. Точкой пересечения они делятся пополам и образуют прямоугольный треугольник с катетами 5 и 12. Гипотенуза этого треугольника - искомый радиус. Треугольник с катетами 5 и 12 из Пифагоровых троек (прямоугольные треугольники с целочисленными сторонами), следовательно, R=13 (можно решить по т.Пифагора с тем же результатом).
* * *
2) Центр шара, вписанного в двугранный угол, равноудален от его сторон, и, следовательно, лежит на биссекторной плоскости, т.е. на плоскости, делящей этот двугранный угол пополам.
Искомое расстояние - диагональ квадрата со сторонами, равными радиусу шара ( биссектриса СО его прямого угла - см. рисунок),
СО=r:sin45°=√2
AC является диагональю квадрата
ПВ и ДВ составляют ВД - вторую диагональ квадрата
По свойству квадрата: диагонали в нём взаимно перпендикулярны!
Следует что ВД перпендикулярно АС; следует ПВ перпендикулярно АС