Объяснение:
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.
Объяснение:
Объем прямой призмы равен произведению площади основания на высоту. Решение данной задачи сводится к нахождению площади трапеции (основания) если известны её основания и боковые стороны.
Найдем высоту трапеции:
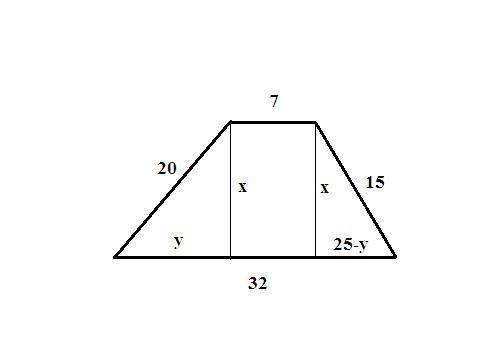
проводим высоты из вершин меньшего основания и обозначим её - х, тогда один отрезок на большем основании - обозначим у, а второй отрезок равен (32-7-у)=(25-у);
треугольники, образованные боковыми сторонами, отрезками большего основания и высотами прямоугольные;
по т. Пифагора:
х²=20²-у²
х²=15²-(25-у)²;
решая данную систему находим у=16, тогда высота - х=12 см;
площадь основания - 12*(7+32)/2=294 см², объем - V=294*2=588 см³.
Так как АВ и CD диаметры, они равны
Пересекаются в точке О, при этом АО=ВО=СО=DO т.к. это радиусы окружности
Угол АОС = углу BCD как вертикальные
Отсюда следует что треугольник АОС = треугольнику BCD по двум сторонам и углу между ними
Отсюда угол САВ = углу АВD => АС параллельна BD
Углы BAD и АВС накрестлежащие, отсюда они равны
Угол АВС = 44 градуса