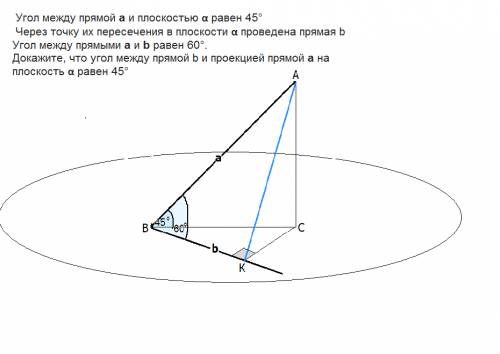
Обозначим начало наклонной А, конец наклонной В ( точка пересечения с плоскостью α).
Опустим из А перпендикуляр на плоскость α.
ВС- проекция наклонной а.
АС⊥ВС.
Угол АВС=45°
Прямую b обозначим ВК; угол АВК=60°
Рассмотрим треугольник АВС.
Так как угол АВС=45°, то угол ВАС=45°,
треугольник АВС прямоугольный равнобедренный.
АС=ВС=а*sin(45°)=(a√2):2.
Треугольник АВК прямоугольный.
ВК=а*cos(60°)=а:2
Треугольник ВКС - прямоугольный с гипотенузой ВС
cos ∠ KBC=BК:ВС=(а:2):(a√2):2=1:√2. Умножив числитель и знаменатель на √2, получим
cos ∠ KBC=√2):2. Это косинус 45°
Е
О
А Д
АС:ВД=3:2, АО:ВО=1,5:1 (диагонали ромба в точке пересечения делятся пополам).
Треугольник ОВЕ подобен треугольнику АЕО (по свойству высоту к гипотенузе прямоугольного треугольника), где ВO и АО гипотенузы. Тогда Saeo/Sobe=(1,5/1)^2
Sobe=27/2,25=12
Saob=Saeo+Sobe=27+12=39
Sabcd=4*Saob=4*39=156
^2-во второй степени