См. Объяснение.
Объяснение:
1-й с шкалированной линейки).
1) Чертим произвольный отрезок.
2) Измеряем длину отрезка (L).
3) Решаем уравнение:
2х + 6х = L
x = L/8.
4) От начала отрезка откладываем:
2х = 2 * (L/8) = L/4 - это и будет точка, разбивающая отрезок в отношении: 2 : 6.
2-й с циркуля и нешкалированной линейки).
1) Чертим произвольный отрезок.
2) Из концов отрезка, раствором циркуля, превышающим половину длины отрезка, делаем по 2 засечки (сверху и снизу).
3) Прикладываем линейку к точкам пересечения засечек и проводим линию, пересекающую отрезок, - это середина отрезка.
4) Аналогично делим пополам, левую половину отрезка и полученную точку отмечаем как границу, которая делит отрезок в отношении 2:6, или, что одно и то же, - 1:3.
( Условие поняла, перевела с переводчика. но ответить могу только на русском, т.к. украинского не знаю)
--------------
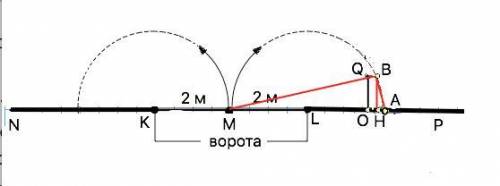
Автомобиль двигался по дороге параллельно забору NP и остановился около закрытых ворот КL так, как изображено на рисунке. Известно, что размах створки ворот LМ составляет 2 м, OQ=1 м. Укажите наименьшую из приведенных длин отрезка LO, при которой створка LM не заденет автомобиль, при условии полного открывания ворот. Считайте, что ворота перпендикулярны плоскости дороги и имеют прямоугольную форму. Толщиной створок пренебречь.
ответ: 1,8 м
Объяснение:
Если автомобиль остановится так, как на рисунке, при полном открывании ворот он будет задет ими задет, т.к. частично. расположен в описываемой створкой полуокружности. .
Решение. От Q вправо проведем прямую до пересечения с линией полуокружности в т.В. От В проведем отрезок ВА ( А - на линии забора).
Треугольник МВА - прямоугольный ( опирается на диаметр МА. Перпендикуляр ВН - высота этого треугольника.
Искомое расстояние - LH.
ВН=QO=1 м по построению. Высота прямоугольного треугольника - среднее пропорциональное отрезков, на которые она делит гипотенузу ( здесь - диаметр МА). =>
ВН²=МН•НА
ML=LA=2 м
Примем LH=x. Тогда МН=2+x, АН= 2-x
(2+х)•(2-х)=1²
4-х²=1 ⇒ х=√3=1,732 ≈1,8 м
Расстояние LO не должно быть менее 1,8 м
Привяжем систему координат к вершине В куба.
Пусть сторона ВС - ось Х, сторона ВВ1 - ось Y, а сторона ВА - осьZ.
Тогда имеем:
Точки В(0;0;0), C(1;0;0), D1(1;1;1)
B1(0;1;0), C(1;0;0) D(1;0;1).
Для составления уравнения плоскости используем формулу:
|x - xB xC - xB xD - xB|
|y - yB yC - yB yD - yB| = 0.
|z - zB zC - zB zD - zB|
Для составления уравнения плоскости CD1A1B
подставим данные трех наших точек B,C и D1:
|х-0 1 1|
|y-0 0 1| = 0.
|z-0 0 1|
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|0 1| |1 1| |1 1|
х*|0 1| - y*|0 1| + z*|0 1| =0.
x*(0-0) - y*(1-0) + z*(1-0) = 0. Или
х*(0)-y*(-1)+z*(1)=0 Это уравнение прямой вида А1х+В1y+C1z=0 с коэффициентами А1=0, В1=-1, С1=1.
Для составления уравнения плоскости DA1B1С
подставим данные трех наших точек B1,C и D:
|х-0 1 1 |
|y-1 -1 -1 | = 0.
|z-0 0 1 |
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|-1 -1| |1 1| | 1 1|
х*| 0 1| - y*|0 1| + z*|-1 -1| =0.
x*(-1-0)) - y*(1-0) + z*(-1+1) = 0. Или
х*(-1)-y*(1)+z*(0)=0 Это уравнение прямой вида А2х+В2y+C2z=0 с коэффициентами А2=-1, В2=-1, С2=0 .
Угол между плоскостями определяется по формуле:
Cosα=|A1*A2+B1*B2+C1*C2|/[√(A1²+B1²+C1²)*√(A2²+B2²+C2²)].
В нашем случае: Cosα=|0+1+0|/[√(0+1²+1²)*√(1²+1²+0)]=1/2.
α=60°.
ответ: искомый угол равен 60°.