8 см - сторона многоугольника;
6 - количество сторон многоугольника.
Объяснение:
Радиус окружности вписанной в многоугольник является перпендикуляром к сторонам данного многоугольника.
Найдем длину стороны многоугольника:
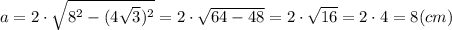
Если из центра окружности провести биссектрисы к углам многоугольника, то многоугольник будет разбит на равные равнобедренные треугольники.
Причем, длины сторон многоугольника равны проведенным биссектрисам (радиусу описанной окружности), т.к. R = 8 см и a = 8 см.
Т.е. многоугольник разбивается на равносторонние треугольники, у которых каждый угол равен 60°.
Найдем количество сторон многоугольника:
n = 360° : 60° = 6.
Проверим найденное количество сторон многоугольника через формулу:
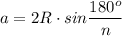
Подставив в формулу величину радиуса описанной окружности и найденное количество сторон многоугольника, должна быть получена длина стороны многоугольника, т.е. 8 см.
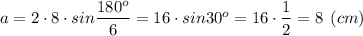
Условие
В выпуклом четырёхугольнике, не являющемся параллелограммом, две противоположные стороны равны.
Докажите, что прямая, проходящая через середины его диагоналей, образует равные углы с этими сторонами.
Решение
Пусть M и N – середины диагоналей соответственно AC и BD выпуклого четырёхугольника ABCD, в котором AB = CD. Если K – середина стороны BC, то KM – средняя линия треугольника ABC, а KN – средняя линия треугольника BCD. Поэтому KM || AB, KM = ½ AB, KN || CD, KN = ½ CD = ½ AB = KM.
Значит, треугольник KMN – равнобедренный. Пусть прямая MN пересекает стороны AB и CD соответственно в точках P и Q. Тогда
∠BPM = ∠KMN = ∠KNM = ∠CQN. Что и требовалось доказать.
Объяснение: