Чтобы узнать, существует ли такой треугольник со сторонам 3; 3; 8 — надо сравнить каждую сторону с суммой друх других сторон: 8+3 = 11.
Каждая сумма двух сторон должна быть больше каждой стороны, чтобы такой треугольник существовал.
Сумма боковый сторон — 3+3 = 6, которая меньше стороны 8, тоесть треугольник со сторонами 3; 3; 8 — не существует.
Теперь представим, что боковые стороны равны 8; 8, а основание — 3.
3+8 = 11 > 3;
8+8 = 16 > 3
8+3 = 11 > 3.
В этом случае, треугольник сущестует, а основание — 3, боковые стороны — 8; 8.
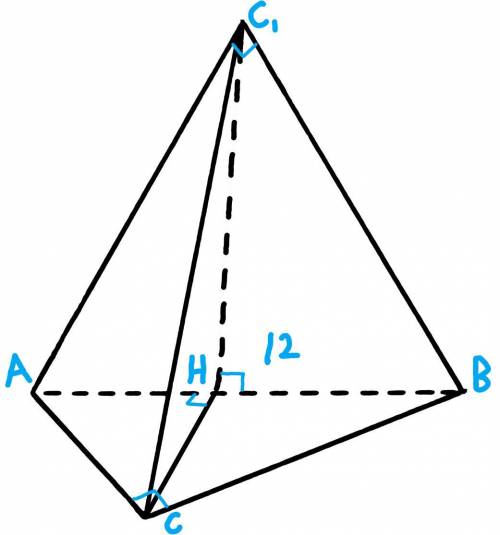
Пусть ABC ⊂ α, а ABC₁ ⊂ β
Две плоскости будут перпендикулярны когда угол между этими плоскостями будет равен 90°
Опустим высоты из вершин C и C₁ на сторону AB. Они пересекутся в точке H.
Следовательно угол между α и β = ∠C₁HC = 90°
Рассмотрим ΔABC
Гипотенуза этого треугольника равна
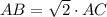
Следовательно
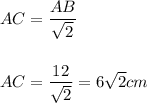
Так как треугольник равнобедренный, то CB = AC = 6√2 см
Найдём площадь треугольника S
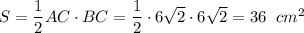
Найдём CH
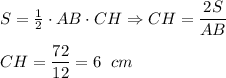
Так как ΔABC₁ - равнобедренный и имеет общую гипотенузу с ΔABC, то ΔABC₁ = ΔABC
ΔABC₁ = ΔABC ⇒ C₁H = CH = 6 см.
Рассмотрим ΔHCC₁
CH = C₁H и ∠C₁HC = 90 ⇒ ΔHCC₁ - прямоугольный, равнобедренный
CC₁ = √2 CH = 6√2 см.
Найти: угол С
Решение: т.к. сумма углов четырехугольника равна 360° и у равнобедренной трапеции углы при каждом основании равны ⇒
тупой угол = (360-98)/2=131°