20см
Объяснение:
1) Стороны (отрезки) обычно обозначаются большими буквами: АС, AD и угол ACD,
а маленькими буквами обозначают, например, прямая а, прямая b и т. д.
2) выч (И) сления = чИсла
ABCD - прямоугольник
АС - его диагональ
Треугольник ACD:
AC = 12 см
AD = 10 см
L ADC = 90 град.
L ACD = 60 град.
=>
L CAD = 180 - (L ADC + L ACD) = 180 - (90 + 60) = 30 град.
Против угла в 30 град. лежит сторона = 1\2 гипотенузы =>
CD = 1\2 * AC = 1\2 * 12 = 6 см - вторая сторона прямоугольника
(хотя если решать по теореме Пифагора, то
CD^2 = AC^2 - AD^2 = 12^2 - 10^2 = 144 - 100 = 44 = 6,63 cм,
но это неточность составителя этой задачи, то есть треугольника с АС = 12, AD = 10 и углом ACD в 60 град. быть не может).
Но раз в условии дан угол, будем считать, что CD = 6 cм.
S (ABCD) = AD * CD = 10 * 6 = 60 см^2 - площадь ABCD
P (ABCD) = 2 * (AD + CD) = 2 * (10 + 6) = 32 см - периметр ABCD
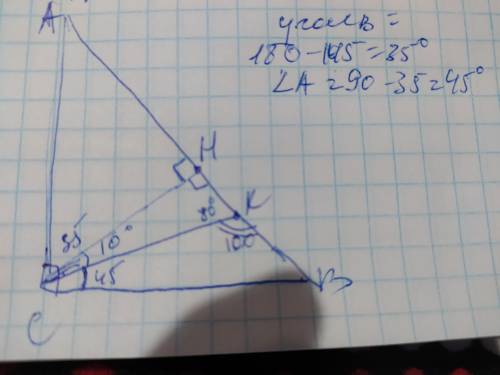
ответ: угол А=45°, угол В=35°
Объяснение: обозначим вершины треугольника А В С, где угол С=90°, высоту–СН, биссектрису СК. Так как биссектриса делит угол С пополам то угол КСВ=45°. Рассмотрим полученный ∆СНК. Он прямоугольный: угол СНК=90°; угол КСН=10°, так как сумма острых углов прямоугольного треугольника составляет 90°, то угол СКН=90-10=80°. Теперь рассмотрим полученный ∆КВС. Угол СКВсмежный с углом СКН и так как сумма смежных углов составляет 180°, то
угол СКВ=180-80=100°. Также в этом треугольнике мы нашли угол КСВ=45°. Так как сумма углов треугольника составляет 180°, то
угол В=180-100-45=35°. Теперь найдём угол А. Угол А=90-35°=45°
1. Осевое сечение цилиндра - прямоугольник.
Из прямоугольного треугольника ABD:
AD = AC · sin 30° = 8 · 1/2 = 4 см - высота цилиндра,
AB = AC · cos 30° = 8 · √3/2 = 4√3 см - диаметр основания.
R = 1/2 AB = 2√3 см
V = Sосн · h = πR²h = π · (2√3)² · 4 = π · 12 · 4 = 48π см³
2. Пусть Н - середина хорды АВ, тогда ОН - медиана и высота равнобедренного треугольника АОВ (ОА = ОВ как радиусы).
Значит ОН = 4 см - расстояние от оси до хорды.
ОН - проекция СН на плоскость основания, значит СН⊥АВ по теореме о трех перпендикулярах.
СН = 13 см - расстояние от центра верхнего основания до хорды.
ΔСОН: ∠СОН = 90°, по теореме Пифагора:
СО = √(СН² - ОН²) = √(13² - 4²) = √(169 - 16) = √153 = 3√17 см - высота цилиндра.
ΔОНВ: ∠ОНВ = 90°, НВ = 1/2 АВ = 3 см, ОН = 4 см, египетский треугольник, ⇒ ОВ = 5 см - радиус основания.
Итак, R = 5 см, h = 3√17 см,
V = Sосн · h = πR²h = π · 5² · 3√17 = π · 25 · 3√17 = 75√17π см³
3. Сечение цилиндра, параллельное оси - прямоугольник.
Пусть Н - середина АВ, тогда ОН - медиана и высота равнобедренного треугольника АОВ (ОА = ОВ как радиусы).
Значит ОН = 4 см - расстояние от оси до сечения.
ΔАОН: ∠АНО = 90°, ОН = 4 см, ОА = 5 см, египетский треугольник, ⇒
АН = 3 см, а АВ = 6 см.
ΔАВС: ∠АВС = 90°, по теореме Пифагора
СВ = √(АС² - АВ²) = √((6√5)² - 6²) = √(180 - 36) = √144 = 12 см - высота цилиндра.
Итак, R = 5 см, h = 12 см,
V = Sосн · h = πR²h = π · 5² · 12 = π · 25 · 12 = 300π см³
4. Провод имеет форму цилиндра, высота цилиндра - его длина.
R = d/2 = 1 мм = 0,001 м
Масса провода:
m = V·ρ
V = m/ρ = 5,6 / (8,9 · 10³) = 56/89 · 10⁻³ м³
Sосн = πR² = π · (10⁻³)² = π · 10⁻⁶ м²
V = Sосн · h
h = V / Sосн
h = 56/89 · 10⁻³ / (π · 10⁻⁶) = 56/(89π) · 10³ м ≈ 200 м
5. Пятно имеет форму цилиндра с высотой 1 мм, объемом 1 м³.
V = 1 м³,
h = 1 мм = 10⁻³ м
Sосн = V / h = 1 / 10⁻³ = 1000 м²