0А=6см
Перпендикуляр и наклонные к
плосксти.
Объяснение:
Дано:
SA, SB - наклонные к
плоскости а
SO - перпендикуляр к а
SB=17см
ОВ=15см
SA=10см
------------------------------------
ОА - ?
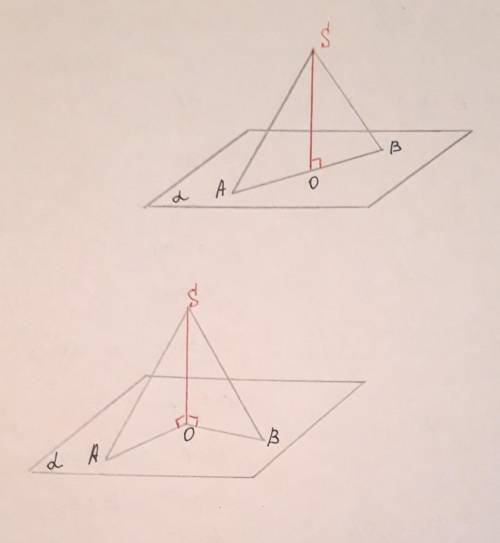
SO - перпендикуляр к плос
кости а ==> SO перпендику
лярна прямым ОВ иОА.
Возможны 2 варианта:
1) точки SAОB лежат в одной
плоскости;
2) точки SAОB не лежат в од
ной плоскости.
Решение и ответ одинаковы
для обоих вариантов.
Рассмотрим треугольник SOB:
<SOB=90°
Треуг. SOB - прямоугольный.
По теореме Пифагора:
SO^2=SB^2-OB^2
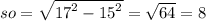
Рассмотрим треугольник SOA:
<SOB=90°
Треуг. SOA - прямоугольный.
По теореие Пифагора:
OA^2=SA^2-SO^2
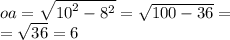
Oтвет:
ОА=6см

1) нет
2) нет
3) нет
Объяснение:
1) Любой четырехугольник - плоская фигура, лежит только в одной плоскости
Не может быть так, что три вершины в одной плоскости, а четвертая в другой
2) Есть такая теорема: Через любые три точки, НЕ принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Если точки принадлежат одной прямой, то плоскостей будет бесконечное множество.
3) Нет, так как если три точки будут принадлежать одной прямой, то все четыре точки будут принадлежать одной плоскости, что противоречит условию
(Надо так повернуть одну из хорд вокруг центра окружности, чтобы две хорды стали параллельны. И сразу видно, что большая хорда стягивает большую дугу)
Поэтому угол треугольника, лежащий напротив большей стороны опирается на большую дугу. Остается вспомнить, как связаны вписанный угол и дуга, на которую он опирается.