Question

Вчетырехугольной пирамиде sabcd все ребра равны. докажите, что плоскость bmd перпендикулярна прямой sc, где m - середина ребра sc

Answer 1

Надо доказать, что углы SMO и SMD прямые

Т.к. все ребра равны (путь a), то треугольник SCD - равносторонний значит DM является и медианой и высотой, т.е. угол DMS=90

Т.к. AB=AD=a то по т. Пифагора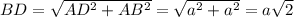 $BD=\sqrt{AD^2+AB^2}=\sqrt{a^2+a^2}=a\sqrt{2}$

Так же по т.Пифагора: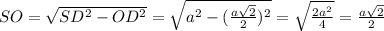 $SO=\sqrt{SD^2-OD^2}=\sqrt{a^2-(\frac{a\sqrt{2}}{2})^2}=\sqrt{\frac{2a^2}{4}}=\frac{a\sqrt{2}}{2}$

Т.к. CO=OD=SO то треугольник SOC равнобедренный, ОМ - медина и высота то угол SMO=90