Объяснение:
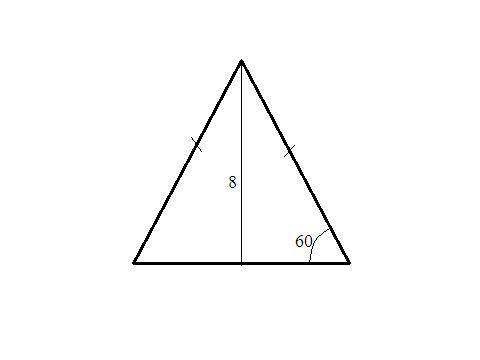
Дано ∆АВС, <С=90
<(СЕ)(АВ)=90
Р(АЕС)=12,. Р(ВЕС)=5
Р(АВС)
Решение.
Р(АВС)=АВ+АС+ВС
Р(АЕС)=АС+АЕ+СЕ)=12
Р(ВЕС)=ВС+ВЕ+СЕ)=5
Для решения системы уравнений вычтим и сложим обе части между собой
Р(АВС)=АВ+АС+ВС;. АВ=АЕ+ЕВ,
12+5=АС+АЕ+СЕ+ВС+ВЕ+СЕ
17= Р(АВС)+2СЕ
12-5=АС+АЕ+СЕ- ВС -ВЕ -СЕ
7 = АС+АЕ -ВС -ВЕ
Воспользуемся свойством высоты прямоугольного треугольника h^2=AE*EB,
AC^2=AE^2+CE^2
BC^2=BE^2+CE^2. вычтим из
АС^2 -BC^2=AE^2 -BE^2
AC^2 + BC^2 = AE^2+2CE^2+BE^2
AB^2=(AE+BE)^2=AE^2+2AE*BE+BE^2
вычтим/сложим одно из/с другого,
2СЕ^2 - 2АЕ*ВЕ;
. СЕ^2=АЕ*ВЕ. CE=AC*BC/AB
2АВ^2=2AE
P(ABC)=17 - 2√(AE*BE)
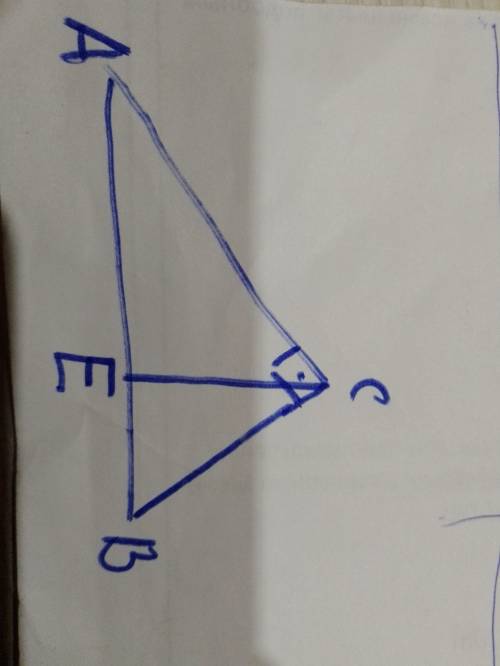
Объяснение:
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.
Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -
(2х)²=8²+х²
х²=8²/3
х=8/√3;
Площадь - S=a*h/2, где а=2х=16/√3, h=8;
S=16*8/(2√3)=64/√3=64√3/3.
Можно проще.
Угол при основании 60° ⇒ треугольник равносторонний.
S=h²/√3=8²/√3=64/√3=64√3/3.