В треугольнике ABC AC= BC, K - точка пересечения биссектрис треугольника, а O - точка, равноудаленная от всех вершин треугольника. Отрезок OK пересекает сторону AB в точке E и точкой пересечения делится пополам. Найдите углы треугольника ABC.
------
Точка К равноудалена от сторон треугольника, поэтому является центром вписанной окружности.
Точка О - равноудалена от вершин треугольника и является центром описанной окружности. Точка К лежит на высоте и медиане к АВ ( на срединном перпендикуляре), точка О лежит на срединном перпендикуляре к АВ, поэтому С, К, Е и О принадлежат одной прямой СО.
Т.к. отрезок КО пересекает АВ, точка О расположена вне треугольника.
Высота и медиана СЕ ⊥ АВ и делит его пополам.
Соединим точки К и О с вершинами А и В.
В получившемся четырехугольнике АКВО отрезки АЕ=ВЕ, КЕ=ОЕ.
Треугольники, на которые КО и АВ делят этот четырехугольник, прямоугольные и равны по двум катетам.
Следовательно, АК=ВК=ВО=АО, и АКВО - ромб. АВ - его диагональ и делит его углы пополам.
Пусть ∠ЕАО=α, тогда ∠КАЕ=α, а, так как АК - биссектриса угла САВ, то ∠САК=∠ЕАК, и ∠САЕ=2α.
∆СОА - равнобедренный ( по условию ОА=ОС=ОВ).
∠ОСА=∠ОАС=3α.
Сумма острых углов прямоугольного треугольника равна 90°.
В ∆ СЕА ∠САЕ+∠АСЕ=5α.
5α=90°, откуда α=90°:5=18°
∠САВ=∠СВА=2•18°=36°
∠АСВ=180°-2•36°=108°.

1.
Правильный ответ: б) Проходит через его вершины.
Вариант а — описывает описанный треугольник.
2.
Правильный ответ: в) центр и любую точку окружности.
3.
Правильный ответ: а) 90°.
Объяснение: касательная имеет теорему, которая гласит, что радиус, проведённый с точки касания — перпендикулярен касательной.
4.
Правильный ответ: а) по одну сторону от.
5.
CA — радиус, проведённый с точки касания, то есть — он перпендикулярен касательной, то есть: он образует прямой угол с ней.
Следовательно: <CAB = 90°.
Один из острых углов: 63° ⇒ <ABC = 90-63 = 27°.
Правильный ответ: а) 27
6.
Так как центр окружности — O, то <BOC — центральный, что означает, что: любой отрезок, проведённый с любой точки окружности до её центра — радиус.
То есть: 
Так как стороны равны, то и углы, прилежащие боковым сторонам — тоже:
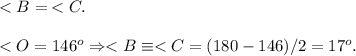
Теперь — проведём высоту OM.
Так как треугольник BOC — равнобедренный, то: высота равна биссектрисе и медиане.
То есть:
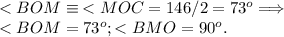
Правильный ответ: вариант б).
7.
Я как поняла, тебе только ответы нужны, да, не объяснение?
Тогда сразу говорю, правильный ответ: вариант в).
8.
Правильный ответ: вариант б).
9.
Правильный ответ: вариант a).
10.
Правильный ответ: вариант в).