Изи
Объяснение:
Задача1:
1)угол MOK(центральный)=дуге MK=78°
2)угол ONK(вписаный)= половине дуги MK=78°:2=39°
3)угол NOK( | радиусу):(по теореме о касательных)
=>(следовательно)=90°
угол x: угол ONK+угол NOK+угол x=180°
( переделаем под угол формулу):
Угол х=180°-(39°+90°)=180°-129°=51°
Задача2:
НЕ ЗНАЮ(((
ПОЯСНЕНИЕ ОБЯЗАТЕЛЬНО ПРОЧИТАЙ,ЧТОБЫ В ДАЛЬНЕЙШЕМ ПОНИМАТЬ,ЧТО Я ПИШУ,ТАК КАК ВРЕМЯ ДЕНЬГИ, ТО:
ВПИСАННЫЙ УГОЛ-В
ЦЕНТРАЛЬНЫЙ УГОЛ0-Ц
РАДИУС-Р
Диаметр-Д
Дуга-д
Угол-У
Половина- п
Известны дуги сумма дуг =360°
=> д KM+д ML+д KL=360°
=> д KL=360°-(д KM+д ML)=360°-(77°+143°)=360°-220°=140°
У M(ВУ:=П д)=140°÷2=70°
Задача10:
Не знаю чего-то не могу увидеть вижу только:
MN-Д
У MKN=90 опирается на Д и по теореме касательных тоже
Будем считать, что задание дано так:
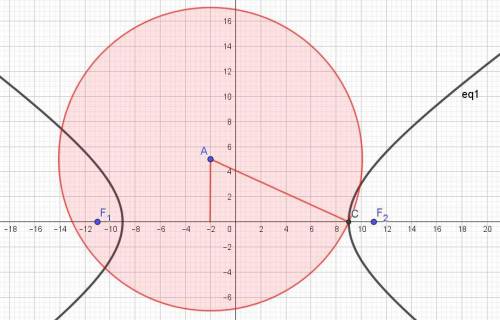
Определить уравнение окружности, проходящей через правую вершину гиперболы 40x² - 81y² = 3240 и имеющей центр в точке А(-2; 5).
Уравнение гиперболы приведём к каноническому виду, разделив обе части заданного уравнения на 3240:
(x²/81) - (y²/40) = 1.
Или так: (x²/9²) - (y²/(2√10)²) = 1 это и есть каноническое уравнение.
Отсюда находим координаты правой вершины гиперболы: С(9; 0).
Теперь находим радиус заданной окружности как отрезок АС.
АС = √((9 - (-2))² + (0 - 5)²) = √(121 + 25) = √146.
Получаем ответ: (x + 2)² + (y - 5)² = 146.
смотри прикрепленный файл