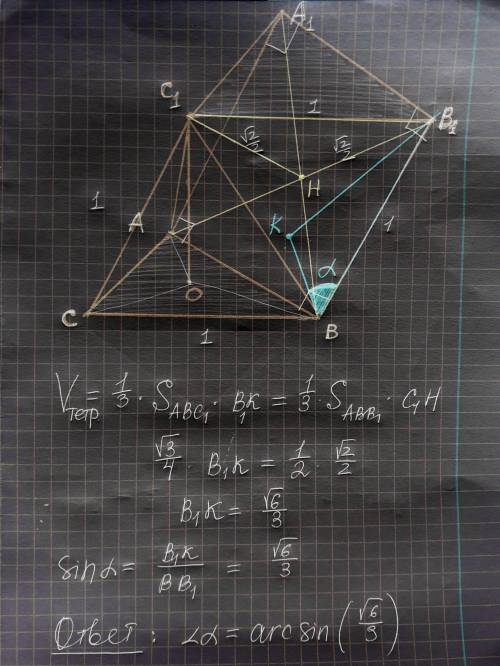
ΔАВС - равносторонний, по условию С₁О - это отрезок, соединяющий центр О основания АВС с вершиной С₁, и перпендикулрный плоскости основания АВС, значит, пирамида C₁ABC - правильная, но не только, это и правильный тетраэдр, пусть все его стороны равны 1, тогда можно заметить, что в пирамиде С₁АВВ₁А₁ в основании лежит ромб, а её высота падает в точку Н - точку пересечения диагоналей ромба, но её боковые грани состоят из правильных треугольников, а значит, что и их прокеции будут равны и ВАУ! мы получаем в основании квадрат! То есть сама изначальная призма состоит из правильного тетраэдра и правильной четырёхугольной пирамиды, все стороны которых равны по 1.
∠(АА₁;(АВС₁)) = ∠(ВВ₁;(АВС₁))
Рассмотрим пирамиду В₁АВС₁ и возпользуемся методом площадей:
C₁H² + B₁H² = B₁C₁² ⇒ C₁H = √2/2 ; S (abc) = √3/2 ; S (abb₁) = 1/2
См. приложение. ответ: arcsin(√6/3)
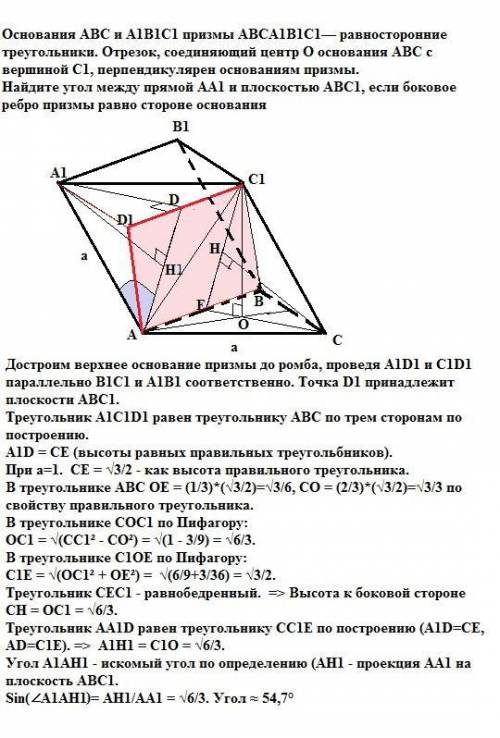
Sin(∠A1AH1) = √6/3. Угол ≈ 54,7°
Объяснение:
Достроим верхнее основание призмы до ромба, проведя A1D1 и C1D1 параллельно B1C1 и A1B1 соответственно. Точка D1 принадлежит плоскости АВС1.
Треугольник А1С1D1 равен треугольнику АВС по трем сторонам по построению.
A1D = CE (высоты равных правильных треугольников).
При а=1. CE = √3/2 - как высота правильного треугольника.
В треугольнике АВС ОЕ = (1/3)*(√3/2)=√3/6,
СО = (2/3)*(√3/2)=√3/3 по свойству правильного треугольника.
В треугольнике СОС1 по Пифагору:
ОС1 = √(СС1² - СО²) = √(1 - 3/9) = √6/3.
В треугольнике С1ОЕ по Пифагору:
С1Е = √(ОС1² + ОЕ²) = √(6/9+3/36) = √3/2.
Треугольник CEC1 - равнобедренный. => Высота к боковой стороне СН = ОС1 = √6/3.
Треугольник АА1D равен треугольнику СС1Е по построению (A1D=CE, AD=C1E). => A1H1 = C1O = √6/3.
Угол A1АН1 - искомый угол по определению (AH1 - проекция АА1 на плоскость АВС1.
Sin(∠A1AH1) = AH1/AA1 = √6/3. Угол ≈ 54,7°
13 ^2 = x^2 + H^2
15^2 = (x+4)^2 + H^2
Имеем два уравнения с двумя неизвестными. Можно решить. Ну так решим же эту систему методами алгебры.
Проще всего сначала будет исключить Н, тогда получим одно уравнение:
15^2 - (x+4)^2 = 13^2 - x^2
225 - x^2 - 8*x - 16 = 169 - x^2
40 = 8*x
x = 5
То есть первая проекция у нас выходит 5 см, вторая, соответственно, 5+4 = 9 см.
Осталось последнее телодвижение - по теореме Пифагора же находим Н = корень ( 13*13 - 5*5) = корень(144) = 12 см -- это ответ.
Ну, у меня так получилось. Лучше проверь, а то с калькулятором не дружу.