Если квадрат и ромб имеют одинаковые периметры, тто они имеют и одинаковые стороны. Воспользуемся следующей формулой для вычисления площади параллелограмма в случае ромба.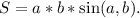 
В данном случае стороны равны, значит формула упрощается до 
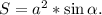. Заметим, что 
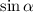Это угол между сторонами ромба. Здесь не имеет значения острый или тупой, так как в обоих случаях будет положительный ответ. Площадь квадрата же всегда равна 
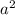. Заметим, что синус всегда меняется в данном случае от 0 до 1. То есть только в случае синуса равного 1 (а это квадрат) площадь ромба равна площади квадрата, в остальных случаях площадь ромба всегда меньше площади квадрата.
1) AB=CD по свойству параллелограмма.
2) треугольник ABK = треугольнику DCK по трём сторонам.
AB=CD по доказанному, BK=KC по условию, AK=DK по условию.
Значит угол ABK= углу DCK.
3) угол ABK + угол DCK =180, т.к. они односторонние при AB||CD и секущей BC.
4) угол ABK= углу DCK=90.
5) ABCD - прямоугольник по признаку.