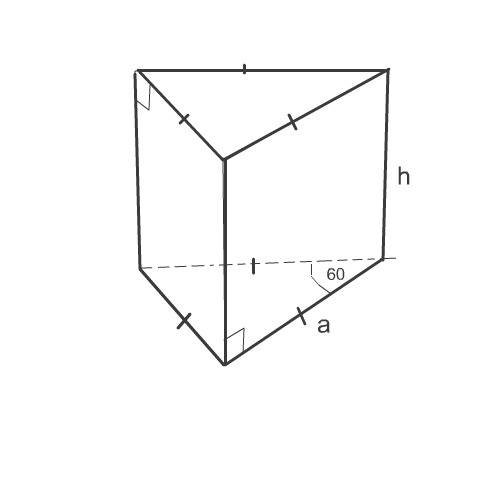
Площадь полной поверхности призмы равна сумме площади боковой поверхности и площадей двух ее оснований, так как в призме оснований два - нижнее и равное ему верхнее.
Найдем площадь оснований.
Основания - правильные треугольники.
Площадь правильного ( равностороннего) треугольника вычисляется по формуле
S осн=а² √3):4
где а - сторона правильного треугольника
S осн=16√3):4=4√3см²
Высоту призмы найдем из ее объема через формулу объема призмы:
V=Sh
36=4√3·h
h=36:4√3=9:√3=9√3):√3·√3=3√3 см
Площадь боковой поверхности призмы вычислим по формуле:
S бок=Р·h,
где Р - периметр основания, h-высота призмы
S бок=3·4·3√3=36√3 см²
Теперь вычислим площадь всей поверхности призмы.
S полн=S бок+ 2 Sоснов
S полн=36√3 +2·4√3=44√3 см²
Добавить вложения
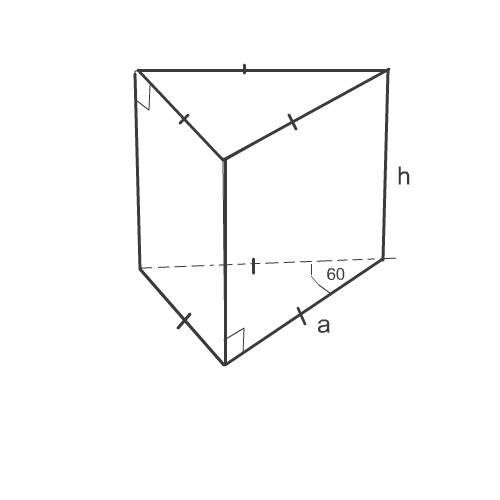
Объем правильной призмы равен произведению площади основания на ее высоту.
V=Sh
Площадь основания можем найти, так как известна сторона основания призмы.
1) Найдем площадь основания призмы по формуле площади правильного треугольника. Если она забыта, можно найти высоту этого треугольника по теореме Пифагора.
Площадь правильного ( равностороннего) треугольника вычисляется по формуле
S осн=а² √3):4
где а - сторона правильного треугольника
S осн =3²√3):4=9√3):4
Высоту найдем из площади боковой поверхности призмы.
2) Найдем высоту призмы из формулы площади боковой поверхности призмы:
S бок=Р·h,
где Р - периметр основания, h-высота призмы.
45=9·h
h=45:9=5 cм
3) Найдем объем призмы:
V=Sh={9√3):4}·5=45√3:4=11,25√3 см³