Объяснение:
а) Пусть СХ=х , тогда ХД=7-х.
Произведение отрезков одной хорды равно произведению отрезков другой хорды ⇒
СХ*ХД=АХ*ХВ,
х*(7-х)=2*6 , 7х-х²=12 ,
х²-7х+12=0, D=49-48=1>0 ,
По т. Виета х₁+ х₂=7
х₁* х₂=12 ⇒ х₁=4, х₂=3 .
Если СХ=4 , тогда ХД=7-4=3.
Если СХ=3 , тогда ХД=7-3=4.
б) ∪ АД=80°, ∪ СВ=48°.∠АХС=180°-∠АХД. Найдем угол ∠АХД по теореме : "Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами " ⇒
∠АХД=(48°+80°):2=64°.
∠АХС=180°-64°=116°.
Дано:
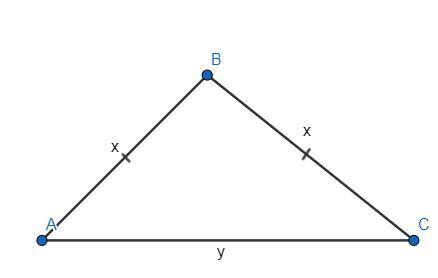
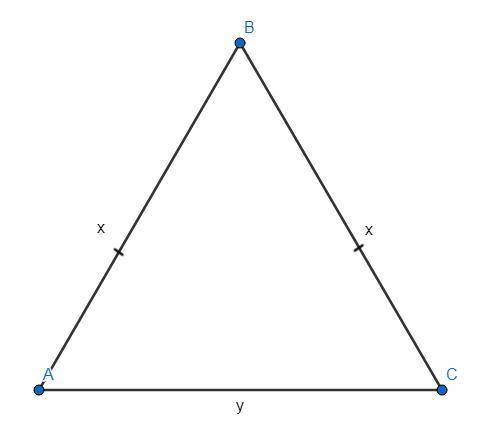
ΔАВС - равнобедренный (АВ и ВС - боковые стороны).
Р(ΔАВС) = 25 см.
Разность двух сторон = 4 см.
Найти:
АВ = ?
ВС = ?
АС = ?
1) Итак, разность боковых сторон АВ и ВС не может быть равна 4 см, так как они равны, и при вычитании должны давать 0.
Тогда, только остаётся, что разность основания АС и боковой стороны АВ = 4 см.
Пусть боковые стороны АВ и ВС = х, а основание АС = у.
Составим систему -
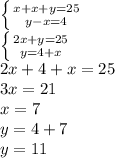
АВ = ВС = х = 7 см.
АС = у = 11 см.
2) Но стоп, вдруг боковая сторона больше основания, тогда получится, что разность боковой стороны АВ и основания АС = 4 см!
Составим новую систему -
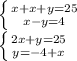
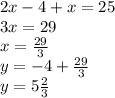
АВ = ВС = х = 29/3 см.
АС = у = 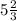 см.
см.
ответ: 7 см, 7 см, 11 см или 29/3 см, 29/3 см, 5+(2/3) см.