если я правильно вас поняла
Объяснение:
https://ru-static.z-dn.net/files/d01/d980879d76ec81b197017dba5b950075.jpg
Пусть M и N, это середины оснований BC и AD равнобедренной трапеции ABCD с перпендикулярными диагоналями AC и BD, K и L — середины боковых сторон AB и CD. Тогда
KM || AC || LN, ML || BD || KN,
поэтому четырехугольник KMLN — прямоугольник. Значит, KL = MN, но KL — средняя линия трапеции, а MN — высота.
Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
Доказательство
Пусть ABCD – данная трапеция. Проведем через вершину B и середину N боковой стороны CD прямую, пересекающую прямую AD в точке F .
Треугольники BCN и FDN равны по теореме 4.2, так как CN = ND, BCN = NDF как внутренние накрест лежащие при параллельных прямых ( BC ) и ( AD ) и секущей ( CD ). CNB = DNF как вертикальные. Из равенства треугольников следует равенство сторон: BN = NF, BC = DF . Средняя линия трапеции MN является средней линией треугольника ABF и по теореме 4.12 ( MN ) || ( AD ) || ( BC ) и Теорема доказана.
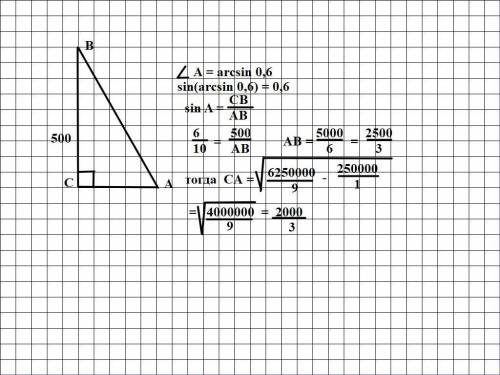
Условие неполное, в зависимости от него ответ 2000/3м или 375м
Объяснение:
sin(CAB)=0,6=3/5
cos(CAB)=sqrt(1-(3/5)^2)=sqrt(16/25)=4/5
tg(CAB)=(3/5)/(4/5)=3/4
Если угол CAB прилежит к катету, равному 500м, то второй катет равен 500/4*3=375м, иначе 500/3*4=2000/3м.