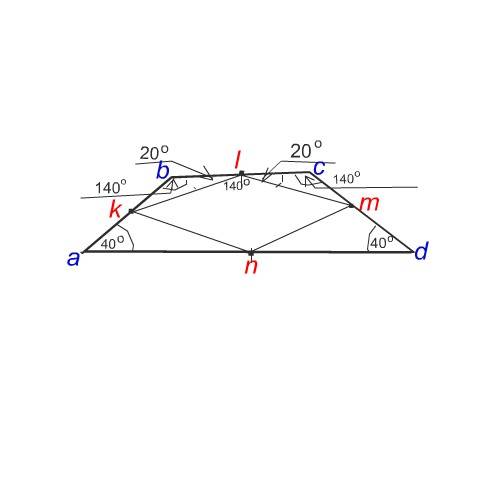
При решении следует учитывать. что трапеция не только равнобедренная, но что и меньшее основание трапеции длиной равно боковым сторонам.
Сделаем рисунок.
Δ kbl равнобедренный, так как kb=bl как половины равных сторон аb и bс
Тупой угол b трапеции равен 180°-40°=140° .
Поэтому сумма углов bkl и blk равна 180°-140°=40°, а каждый из них равен 20° .
Углы треугольника lcm равны по величине углам треугольника bkl, так как сами эти треугольники равны.
Отсюда величина угла klm, большего в четырехугольнике klmn, равна 180°-40°=140°
Дано: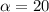 
градусов - вписанный угол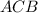 
Пусть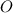 
- центр данной окружности
Тогда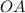 
- радиус данной окружности и тогда по свойству касательной
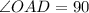градусов-------(*)
Рассмотрим треугольник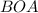 
. Этот треугольник равнобедренный (
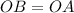как радиусы). Поэтому по признаку равнобедренного треугольника имеем:
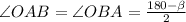------(1)
где 
- градусная мера центрального угла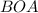
Из свойства вписанного угла имеем:
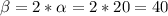градусов--------(2)
Подставим в (1) вместо 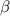его значение:
угол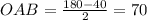 
градусов-------(3)
По основному свойству измерения углов найдем искомый угол:
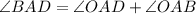--------(4)
C учетом равенств (*) и (3) равенство (4) примет вид:
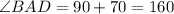градусов
x+x+x+3=45
3x=45-3
3x=42
x=14;
14+3=17-основание
ответ: боковые стороны= 14см, основание= 17см.