Если в четырехугольнике диагонали перпендикулярны, значит он делится ими на четыре прямоугольных треугольника и его площадб равна сумме площадей этих четырех треугольников. Площадь прямоугольного треугольника равна половине произведения его катетов. Следовательно, площадь нашего четырехугольника равна половине произведению его диагоналей. Пусть четырехугольник АВСД и точка пересечения взаимно перпендикулярных диагоналей О. Тогда площадь нашего четырехугольника S = 0,5AO*BO + 0,5OC*BO + 0,5AO*OD + 0,5OC*OD = 0,5BO*(AO+OC) + 0,5OD*(AO+OC) = (AO+OC)*(0,5BO+0,5OD) = AC*BD. Что и требовалось доказать.
Если в четырехугольнике диагонали перпендикулярны, значит он делится ими на четыре прямоугольных треугольника и его площадб равна сумме площадей этих четырех треугольников. Площадь прямоугольного треугольника равна половине произведения его катетов. Следовательно, площадь нашего четырехугольника равна половине произведению его диагоналей. Пусть четырехугольник АВСД и точка пересечения взаимно перпендикулярных диагоналей О. Тогда площадь нашего четырехугольника S = 0,5AO*BO + 0,5OC*BO + 0,5AO*OD + 0,5OC*OD = 0,5BO*(AO+OC) + 0,5OD*(AO+OC) = (AO+OC)*(0,5BO+0,5OD) = AC*BD. Что и требовалось доказать.
общая формула для нахождения радиуса описанной окружности правильного многоугольника
R=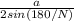 где а-сторона многоугольника, N-количество сторон
где а-сторона многоугольника, N-количество сторон
находим радиус для нашено случая 6-ти угольника
а=48/6=8м
R=8/(2sin30°)=8
теперь рассмотрим случай квадрата
для него радиус тот же
8=а/(sin180/4)=а/sin45
а=8*sin45=8*√2/2=4√2