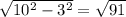. Значит, вся диагональ -- 
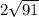, а сторона квадрата, которая в 
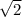раз меньше, чем диагональ, равна 
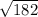. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 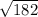. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 
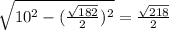, откуда площадь одного треугольника равна 
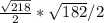, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 
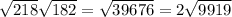Может, обсчитался где-то.
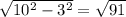. Значит, вся диагональ -- 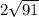, а сторона квадрата, которая в 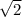раз меньше, чем диагональ, равна 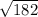. Таким образом, боковая грань представляет собой треугольник со сторонами 10, 10, 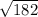. Площадь этого треугольника можно найти, например, опустив высоту из вершины, (эта высота будет и медианой). Получается, высота равна 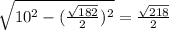, откуда площадь одного треугольника равна 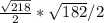, а площадь боковой поверхности равна площади четырёх таких треугольников, т. е. 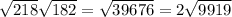Может, обсчитался где-то.
Решение
Площадь боковой поверхности призмы равна произведению ее высоты на периметр основания.
Сумма углов при одной стороне параллелограмма равна 180°
Следовательно, < АВС = 180° - 30° = 150°
Пусть АВ = 4см
ВС = 4√3 см
Найдем по теореме косинусов диагональ основания АС.
АС² = АВ² + ВС² - 2*АВ*ВС* cos (150°)
косинус тупого угла - число отрицательное.
АС² = 16 + 48 + [32√3*(√3)]/2=112
АС = √112 = 4√7
Высота призмы
СС₁ = АС / ctg(60°)=(4√7) / 1/√3
CC₁ = 4√21
Площадь боковой поверхности данной призмы
S = H*P = 4√21*2(4+4√3) = 32√21*(1+√3) см²
ответ: 32√21*(1+√3) см²