Объяснение:
Бічна сторона рівнобедреного трикутника дорівнює 13см, а висота, проведена до основи, – 12 см. Знайдіть:
а) основу трикутника; По Пифагору: половина основания равна
√(13²-12²) = 5 см. Основание = 10 см.
ответ: 10 см.
б) довжину середньої лінії, паралельної основі;
Средняя линия равна половине стороны, параллельно которой она проведена.
ответ: 5 см.
в) косинус кута при основі трикутника;
Косинус угла при основе равен отношению прилежащего катета (половина основания) к гипотенузе (боковая сторона).
ответ: CosA = 5/13.
г) площу трикутника;
Площадь треугольника равна S = (1/2)*AC*h = (1/2)*10*12 = 60 см².
ґ) радіус вписаного кола.
Радиус вписанной окружности равен r = S/p, где S =60см²- площадь, р - полупериметр = (13+13+10):2 = 18см.
ответ: r = 60/18 = 3и2/9 см.
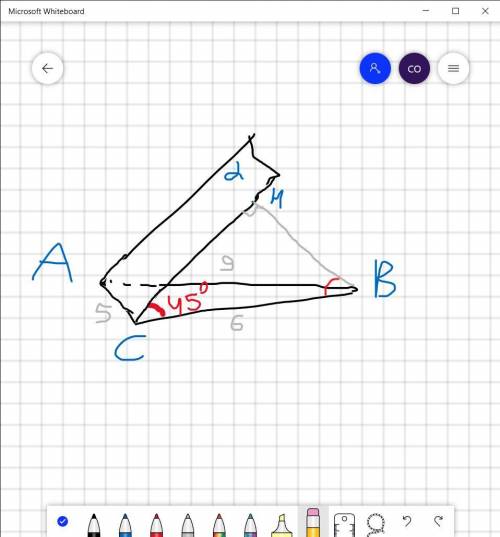
Дано: ΔABC
<(α,ABC)=45°
AB=9см ;BC = 6 см; AC = 5 см
α∩ABC =AC
BH⊥α
Знайти: BH
Розв'язання
ВС-похила до площини α, а ВН-перпендикуляр (оскільки відстань від точки до площини це перпендикуляр проведений із неї до цієї площини), тоді НС-проєкція.
Отже, проєкція похилої НС до площини трикутника ΔABC лежить на відрізку СВ => <HCB=<(α,ABC)=45°
Отримуємо прямокутний трикутник ΔВНС із прямим кутом <СНВ.
Знайдемо невідомий кут <НВС=90°-<HCB=90°-45°=45°
<HCB=<НВС, отже трикутник ΔВНС рівнобедрений і позначимо рівні сторони НС=НВ=х
За теоремою Піфагора
НС²+НВ²=СВ²
х²+х²=6²
2х²=36 | : 2
x²=18
x₁= -√18 (сторонній корень)
х₂=√18=√(9*2)=3√2 см
Відповідь: 3√2 см
(сподіваюся, що правильно)
a²+a²=100², по т. Пифагора, т.к. в основании равнобедренный прямоугольный треугольник
2*a²=10000
a²=5000
Sосн=0,5*5000=2500
V=(1/3)*S*H=(1/3)*90*S=30*2500=75000