т синусов
напротив стороны в 6 см лежит третий угол , равный 180-60-45=75
6/sin75=a/sin60=b/sin45
sin75=sin(45+30)=sin45*cos30+cos45*sin30=V2/2*V3/2+V2/2*1/2=
=(V6+V2)/4
V-знак корня
6/sin75=6:(V6+V2)/4)=24/(V6+V2)
a)если 6/sin75=a/sin60, то
24:(V6+V2)=a:(V3/2)
24*V3/2=a(V6+V2)
12V3=a(V6+V2)
a=12V3/(V6+V2)- чтобы избавиться от иррациональности в знаменателе-домножу дробь на V6-V2
тогда a=12V3*(V6-V2)/(6-2)=3V3(V6-V2)=3V18-3V6
a=9V2-3V6-вторая сторона
b)6/sin75=b/sin45
24:(V6+V2)=b:(V2/2)
24/(V6+V2)=2b/V2
24V2=2b(V6+V2)
b=24V2/(2(V6+V2))=12/(V3+1)-избавляюсь от иррациональности в знаменателе, домножив дробь на V3-1 (и числитель и знаменатель-тогда значение дроби не изменится)
b=12(V3-1)/(3-1)=6(V3-1)=6V3-6-третья сторона
P=6+9V2-3V6+6V3-6=9V2-3V6+6V3
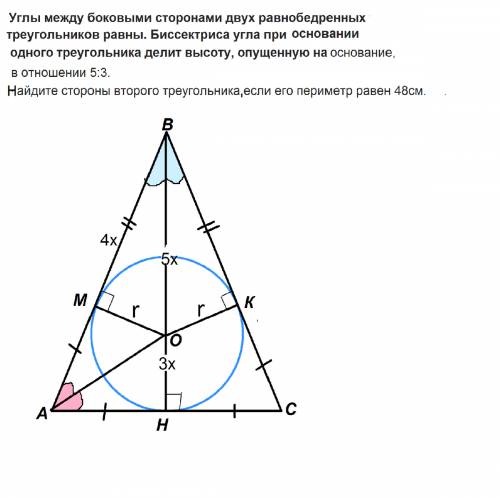
Пусть дан один равнобедренный треугольник и второй равнобедренный треугольник АВС с равными углам при основаниях, следовательно, и третий угол при вершине одного треугольника равен третьему углу второго.
Эти треугольники подобны. В подобных треугольниках все их элементы пропорциональны, следовательно, точка пересечения биссектрисы угла при основании с высотой второго треугольника делит ее в том же отношении, что в первом, т.е. 5:3
Высота ВН равнобедренного треугольника, проведенная к основанию, является и биссектрисой и медианой. АН=НС.
Имеем две биссектрисы треугольника АВС, которые пересекаются в некой точке О. Точка О пересечения биссектрис треугольника АВС является центром вписанной в него окружности.
Из точки О проведем перпендикуляры ОМ и ОК к боковым сторонам треугольника. М, К и Н - точки касания окружности и сторон треугольника.
ОМ=ОК=ОН= радиусу вписанной окружности.
Пусть коэффициент отношения отрезков высоты равен х.
Тогда ВО=5х, ОН=3х, ОМ=ОК=3х
Треугольники ВОМ и ВОК - египетские,т.к. катет и гипотенуза относятся как 3:5 ⇒
ВМ=ВК=4х ( можно проверить по т.Пифагора)
ВН=3х+5х=8х
Треугольники ВМО и ВНА - подобные, т.к. оба прямоугольные и имеют общий острый угол. Следовательно, треугольник ВНА тоже египетский, и из отношения сторон такого треугольника следует
АВ=10х, АН=6х. Или из подобия треугольников через отношение сходственных сторон
ВН:ВМ=АН:ОМ
ВН=3х+5х=8х
8х:4х=АН:МО
АН:МО=2
АН=6х
АВ=ВС=5*2=10х
ВН - медиана, поэтому
АС=6х+6х=12х
Периметр треугольника равен АВ+ВС+АС=48
Р=10х+10х+12х=32х
32х=48
х=1,5 см
АВ=ВС=1,5*10=15 см
АС=1,5*12=18 см