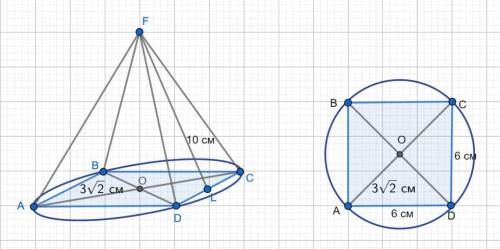
ответ: боковая поверхность заданной пирамиды равна 120 см².
Решение.
Дана правильная четырехугольная пирамида. в основании ее лежит квадрат. Точка пересечения диагоналей квадрата является центром описанной около квадрата окружности, а радиус ее равен половине диагонали квадрата.
Так как радиус описанной окружности AO = 3√2, то диагональ квадрата AC = 2*3√2 = 6√2.
Найдем сторону квадрата ABCD по т.Пифагора:
AC² = AD² + CD² = 2AD²; (6√2)² = 2AD²; 36*2 = 2AD²; AD² = 36; AD = 6 см.
Сторона квадрата = 6 см. Периметр основания пирамиды P = 4AD = 4*6 = 24 см.
Боковая поверхность пирамиды равна половине произведения периметра основания на апофему.
Sбок = (1/2) * P * h = 1/2 * 24 * 10 = 120 (см²).
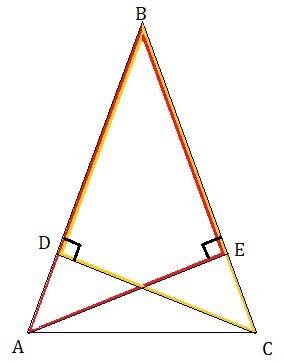
∠BEA = ∠BDC = 90° (так как AE и CD — высоты △ABC).
⟹ треугольники ABE и CBD прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°.
В треугольнике ABE ∠BAE = 90° — ∠B.
В треугольнике CBD ∠BCD = 90° — ∠B.
⟹ ∠BAE = ∠BCD, ∠B — общий,
BA = BC (как боковые стороны равнобедренного △ABC)
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
⟹ треугольники ABE и CBD равны.
Из равенства треугольников следует равенство соответствующих сторон: AE = CD.
Что и требовалось доказать.