Проекции катетов на гипотенузу прямоугольного треугольника - это отрезки гипотенузы, на которые ее делит высота, т.к. высота - перпендикуляр к прямой ( гипотенузе), а катеты – наклонные из вершины прямого угла.
Катет - среднее пропорциональное между гипотенузой и его проекцией на неё .
В треугольнике на рисунке приложения
Катет Вс=30 см, а ВН=18 - его проекция на гипотенузу.
BC²=АВ•НВ
900=АВ•18
АВ=900:18=50 см
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные. Из подобия следует отношение:
АН:АС=АС:АВ
АН=50-18=32
32:АС=АС:50 ⇒ АС²=32•50
АС=√1600=40 см
-----------
Если обратить внимание на отношение катета и гипотенузы 3:5 в ∆ ВСН, увидим, что этот треугольник - египетский. Отсюда следует АВ=50 см, (т.к. меньший катет=30). а АС=40 см. Получим длины сторон треугольника, отношение которых 3:4:5.

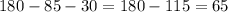
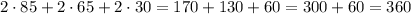
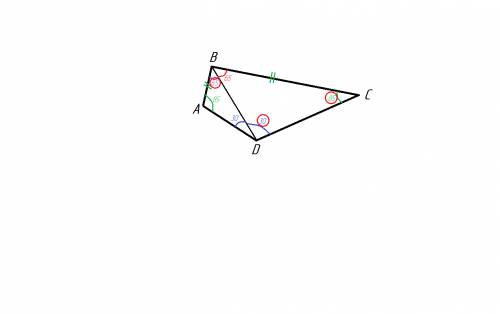
по теореме Чевы
bp / pc * mc / am * al / lp = 1
bp * al / (pc * lp) = 1
bp / pc = lb / al => по теореме, обратной теореме Фалеса lp || ac
также bk / km = 4 => по теореме Фалеса bl / la = bp / pc = 4
Sabk / Sabm = 4 / 5, тк bk / bm = 4 / 5
Sabk = (4 / 5) Sabm
Δbkp ~ Δbmc по двум сторонам и углу между ними => Sbkp / Sbmc = 16 / 25
Skpcm = Sbmc - Sbkp = Sbmc - (16 / 25) * Sbmc = (9 / 25) Sbmc
Sabm = Sabc, тк BM - медиана =>
Sabk / Skpcm = 4 * 25 / (5 * 9) = 20 / 9
ответ: 20 / 9.