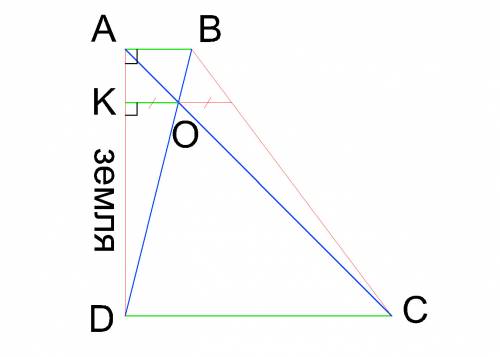
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Один.
2. Из каких точек состоит отрезок AB?
Из всех точек прямой, расположенных между точками А и В, и самих точек А и В.
3. Какие два отрезка называют равными?
Которые можно совместить наложением.
4. Какие длины имеют равные отрезки?
Равные отрезки имеют равные длины.
5. Что можно сказать об отрезках, имеющих равные длины?
Что они равны.
6. Сформулируйте основное свойство длины отрезка.
Длина отрезка равна сумме длин его частей.
7. Можно ли любой отрезок выбрать в качестве единичного?
Да, можно.
8. Что называют расстоянием между двумя точками?
Длину отрезка, с концами в этих точках.
9. Чему равно расстояние между двумя совпадающими точками?
Нулю.
10. Какую точку называют серединой отрезка AB?
Точку, которая делит его на два равных отрезка.