Задача 1
угол АВС= 180- угол КВС=180-108=72°(т.к смежные углы в сумме дают 180°)
угол ВСА=180- угол ВСD= 180-137=43°(т.к смежные углы в сумме дают 180°)
угол А=180- угол АВС- угол ВСА=180-72-43=65°(сумма всех углов в треугольнике равна 180°)
ответ:65; 72;43
Задача 2
внешний угол равен сумме двух противоположных внутренних
Угол С= угол А + угол В
145=3х+17+7х+28
-10х=-100
х=10
Угол А = 3х+17°=30+17=47°
ответ:47°
Задача 3
Угол А внешний= углу САВ=60° (т.к вертикальные)
Угол В=180- угол САВ - -уголС=180-60-90=30
Опустим высоту СК
т.к угол В=30°, то СК=1/2ВС=3,9(т.к катет лежащий против 30° равен половине гипотенузы)
ответ: 30; 3,9
S = 50 ед².
Объяснение:
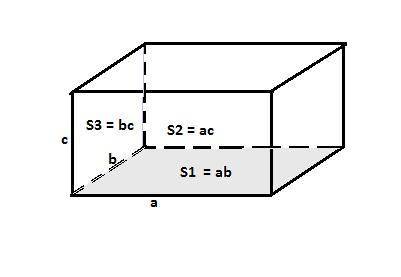
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².
Прямоугольник
Параллелограмм
Трапециевидные
Ромб