2 )Строишь отрезок любой из заданных величин.Затем из концов отрезка строишь окружности , радиусы которых равны двум оставшимся.Точка пересечения этих окружностей будет третей вершиной.Соедини точку с концами отрезка и получишь искомый треугольник.
3) Побудова:
а) будуємо відрізок АВ = 6 см;
б) з обох його кінців А і В як з центрів проводимо кола, радіуси яких дорівнюють АС = 5 см і ВС = 4 см;
в) сполучаємо точки АіВ відрізка АВ з однією із точок С перетину кіл. Трикутника ABC - шуканий.
2) Побудова:
а) будуємо відрізок АВ - 2 см;
б) з обох його кінців А і В як з центрів проводимо кола, радіуси яких дорівнюють АС = ВС = 2 см;
в) сполучаємо точки АіВ відрізка АВ з однією із точок С перетину кіл. Трикутник ABC - шуканий.
а 1 я не знаю(
Объяснение:
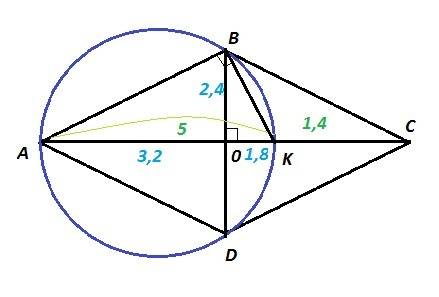
Ромб ABCD, окружность проходит через точки A, B, C
AK = 5 см; КС = 1, 4 см ⇒ АС = АК + КС = 5 + 1,4 = 6,4 см
У ромба диагонали перпендикулярны и точкой пересечения делятся пополам : AC⊥BD; AO=OC = AC/2 = 6,4 /2 = 3,2 см; BO=OD.
AK⊥BD и делит хорду BD пополам ⇒ AK - диаметр окружности.
ΔABK - прямоугольный, так как сторона AK является диаметром описанной окружности.
Высота треугольника, проведенная из прямого угла на гипотенузу, есть среднее геометрическое проекций катетов на гипотенузу :
BO² = AO·OK = AO·(AK-AO) = 3,2·(5-3,2) = 3,2·1,8 = 5,76 = 2,4²
BO = 2,4 см
ΔAOB образован диагоналями, прямоугольный. Теорема Пифагора
AB² = AO² + BO² = 3,2²+2,4² = 10,24+5,76= 16 = 4²
AB = 4 см
ответ: сторона ромба равна 4 см
Прямоугольник АВСД: ВД - гипотенуза = 13см; АВ = СД = 5см
Прямоугольные треугольники АВД и СДВ:
ПО теореме Пифагора рассчитываем катет АВ: АD^2 = BD^2 - AD^2
AD^2 = 169 - 25 = 144
AD = 12cм
S = a*b
S = AB * AD
S = 12 * 5 = 60cм^2