1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение:
Диагонали ромба точкой пересечения делятся пополам (как и у параллелограмма)
Диагонали ромба взаимно перпендикулярны
Диагонали ромба являются биссектрисами его углов
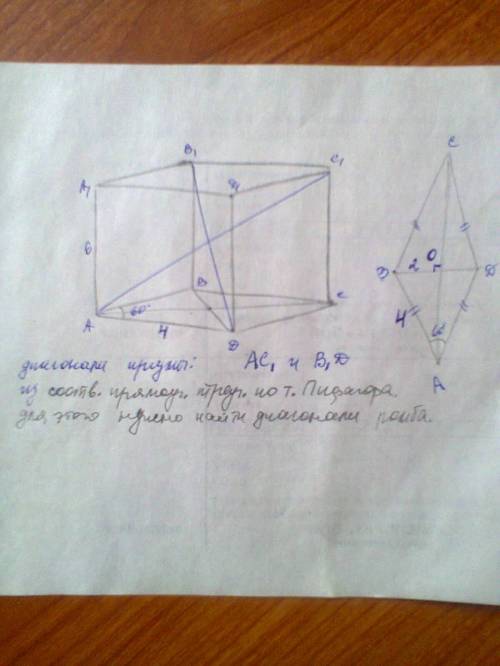
из треуг.BOA: угол BAO=30, катет BO = 4/2 = 2 (катет против угла в 30 град.=половине гипотенузы) и по т.Пифагора второй катет = корень(4^2-2^2) = 2корень(3)
следовательно, диагонали ромба равны
BD = 2BO = 4
AC = 2AO = 4корень(3)
AC1^2 = AC^2 + CC1^2 = 4*4*3 + 6*6 = 4*(12+9) = 4*21
AC1 = 2корень(21)
B1D^2 = BD^2 + CC1^2 = 4+36 = 40
B1D = 2корень(10)
опустим высоту ВН. получим прямоугольный треугольник АВН. АН =
= (АД - ВС) / 2 = 3
По теореме Пифагора ВН = 4
тогда косинус ВАН = 3/5 = 0,6
В АВД найдем ВД по теореме косинусов
ВД^2 = 5 * 5 + 7 * 7 - 2 * 5 * 7 * 0,6 = 25 + 49 - 42 = 32
ВД = 4√2
Площадь треугольника:
S = 1/2ah = abc/4/R
Подставим наши значения
1/2 * 7 * 4 = 5 * 7 * 4√2 / 4 / R
14R = 35√2
R = 5√2 / 2
Площадь круга
πR^2 = π * 25 / 2