
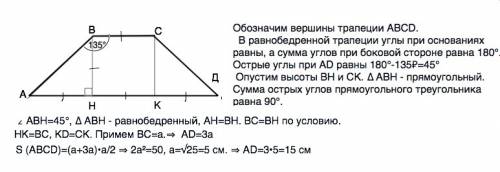
Обозначим вершины трапеции АВСD. В равнобедренной трапеции углы при основаниях равны, а сумма углов при боковой стороне равна 180°.
Острые углы при АD равны 180°-135₽=45°
Опустим высоты ВН и СК. ∆ АВН - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°.
∠ АВН=45°, ∆ АВН - равнобедренный, АН=ВН. ВС=ВН по условию. НК=ВС, КD=СК. Примем ВС=а.⇒ АD=3а
S (АВСD)=(а+3а)•a/2 ⇒ 2a²=50, a=√25=5 см. ⇒ АD=3•5=15 см
Найдем по теореме Пифагора диагональ основания параллелепипеда.
BD= 5^2+6^2=25+36= корень 61
Найдем высоту параллелепипеда
ВВ1 = корень 65-61=корень 4 =2
S =(5*6+5*2+6*2)*2=(30+10+12)*2=52*2=104см^2