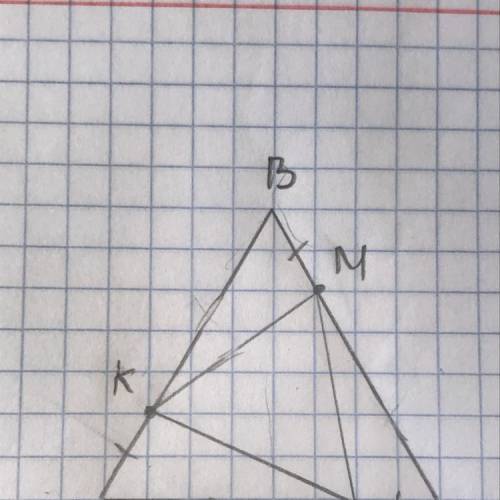PK и AB являются скрещивающимися прямыми, так по-моему называются две прямые в пространстве, которые не пересекаются и не параллельны. Доказывается от противного. Предположим, что параллельны, следовательно лежат в одной плоскости. Но AB - сторона треугольника ABC, следовательно лежит в плоскости треугольника ABC. PK проходит через две точки, принадлежащие треугольнику ACD (это середины сторон AD и CD), следовательно лежит в плоскости треугольника ACD. Но по условию, плоскости треугольников различны, и поэтому прямые PK и AB лежат в разных плоскостях, а значит не параллельны. Пересекающиеся прямые также лежат в одной плоскости, аналогично доказывается что в нашем случае такого быть не может. Остаётся только одна альтернатива - PK и AB - две прямые в пространстве, не параллельные и непересекающиеся.
Вот так, а на часть б) может кто другой ответит, кому не лень всё это чертить и считать.
1) KB = AB - AK => KB = MC = AP (так так треугольник АВС равносторонний по условию, => АВ = ВС = АС, и так так уже дано, что АК = ВМ = СР)
2) угол В = углу А = углу С (так как в равностороннем треугольнике все углы равны)
3) Из этого следует, что треугольник АКР = треугольнику МРС = треугольнику КВМ по двум сторонам и углу между ними
4) Так как мы доказали, что треугольники равны, то и их стороны тоже равны, => все стороны треугольника КМР равны (КР = КМ = МР). Он равнобедренный по определению.