Якщо у прямокутного трикутника катети дорівнюють 3 і 4 см, то трикутник є єгипетським, а отже його гіпотенуза дорівнює 5 см. Перевірити це можна за теоремою Піфагора.
c=√
c=√
c=√
c=√25
c=5 (см)
Синус-відношення протилежного катета до гіпотенузи
якщо треба знайти синус кута, прилеглого до більшого катета, то протилежний до кута катет дорівнює 3 см, а отже
т.к. это египетский треугольник, то гипотенуза равна 5 см. Угол, прилежащий к большему катету, лежит против меньшего катета, равного 3 см, поэтому синус этого угла равен 3/5=0,6
При пересечении двух параллельных прямых АС и РI секущей АI образуются равные накрест лежащие углы <CAI=<AIP. Т.к. АI - биссектриса, то <CAI=<PAI. Из этого следует, что углы при основании <AIP=<РAI, значит ΔАРI - равнобедренный (AP=РI). Аналогично при пересечении двух параллельных прямых ВС и QI секущей BI образуются накрест лежащие углы <CBI=<QIB. Т.к. ВI - биссектриса, то <CВI=<QBI. Из этого следует, что углы при основании <QIB=<QBI, значит ΔQBI - равнобедренный (QB=QI). Периметр ΔРQI равен: Рpqi=PI+PQ+QI=AP+PQ+QB=AB=12
Якщо у прямокутного трикутника катети дорівнюють 3 і 4 см, то трикутник є єгипетським, а отже його гіпотенуза дорівнює 5 см. Перевірити це можна за теоремою Піфагора.
c=√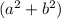
c=√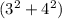
c=√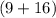
c=√25
c=5 (см)
Синус-відношення протилежного катета до гіпотенузи
якщо треба знайти синус кута, прилеглого до більшого катета, то протилежний до кута катет дорівнює 3 см, а отже
sinα= =0,6
=0,6