Объяснение:
Очевидно, что внутри отрезка AB такой точки существовать не может (если бы существовало, тогда сумма двух меньших отрезков должна быть больше длины исходной, что является противоречием), поэтому эта точка должна лежать где-то за пределами отрезка (по условию же сказано, что нужно найти точки на прямой, а не внутри отрезка).
Пусть l - расстояние от искомой точки X до A, тогда l + 6 - это расстояние от X до B. Тогда справедливо уравнение:
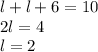
Значит, точка X должна отстоять от точки A на 2 см
Выглядит схематично это так:
2см 6см
---------------|----------------|------------------------------------------|----------------->
X A B
Это справедливо и для случая:
6см 2см
------------------|------------------------------------------|-------------|--------->
A B X
Больше таких точек нет.
1 этап:
Точка, прямая, окружность.
2 этап:
1. На плоскости нужно отметить произвольную точку
2. Через эту точку провести прямую произвольной длины
3. Взять циркуль и провести окружность с центром в точке, которую мы построили в 1 пункте
4. Отметить точки пересечения нашей окружности из 3 пункта и прямой (точки А и B) - это будут крайние точки нашего основания.
5. Не изменяя раствора циркуля провести из точек А и B окружности, точка пересечения этих окружностей будет 3 вершиной равнобедренного треугольника.
6. Соединить 3 полученные точки.
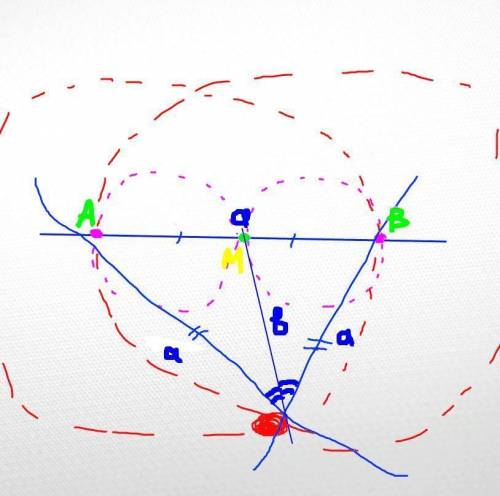
3 этап:
Пусть AB = a.
Отметим на нашем основании точку М = b ⋂ a. По рисунку эта точка совпадает с точкой пересечения окружностей, которые мы провели из крайних точек основания: точек А и B.
АМ = BM (как радиусы равных окружностей), а значит т.М совпадает с точкой пересечения медианы и основания. Отсюда, так как медиана совпадает с биссектрисой треугольник является равнобедренным.
4 этап:
Да, всегда будет иметь решения.
M,N-середины AD,BC⇒MN_|_AD U MN_|_BC⇒AD||BC⇒
ABCD-равнобедренная трапеция
Проведем BH_|_AD,BH=MN=3см MN=1/2*AB⇒<A=30гр и <D=30гр
Значит треугольник АОD равнобедренный
<AOD=180-2<A=180-2*30=180-60=120гр