В объяснении.
Объяснение:
1. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+3х+4х = 360° => х = 36°.
Больший угол равен 4х = 144°.
2. Сумма внутренних углов выпуклого четырехугольника равна 360 градусов.
Пусть коэффициент пропорциональности равен х.
Тогда х+2х+2х+4х = 360° => х = 40°.
Меньший угол равен 4х = 40°.
3. Площадь квадрата равна площади прямоугольника: 4*9 = 36 =>
Сторона квадрата равна √36 = 6 ед.
4. Площадь прямоугольника равна х*(х+2) = 24. Тогда
х² + 2х - 24 = 0. Решаем квадратное уравнение. => x = 6. (второй корень отрицательный)
Тогда большая сторона равна 6 + 2 = 8 ед.
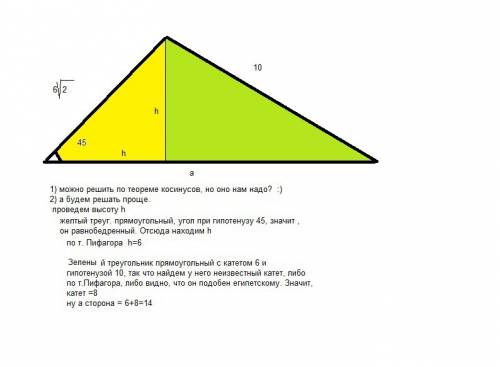
5. Смотри рисунок.
6. Уравнение окружности:
(Х - Хц)² + (Y-Yц)² = R² Тогда
а) Координаты центра: Ц(-5;2) Радиус = 4 ед.
б) Координаты центра: Ц(0;-3) Радиус = 3 ед.
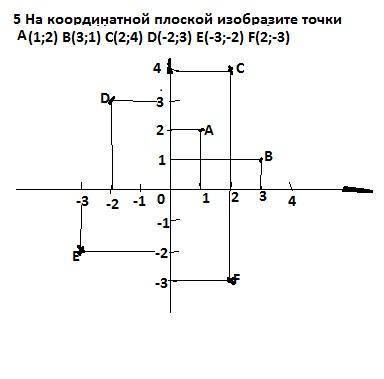
найдем координаты середины диагоналей четырехугольника ABCD:
середина диагонали АС
x=(0+5)/2=2.5
y=(1+1)/2=1
(2.5;1)
середина диагонали BD
x=(4+1)/2=2.5
y=(3+(-1))/2=1
(2.5;1)
таким образом диагонали четырехугольника пересекаются в точке, что делит их пополам, поэтому за признаком парарлелограмма четырехугольник АВСD - парареллограм
найдем длины диагоналей
AC=((5-0)^2+(1-1)^2)=5
BD=((4-1)^2+(-1-3)^2)=5
диагонали параллелограма ABCD равны АC=BD, за признаком прямоугольника ABCD- прямоугольник. Доказано
Подробнее - на -
Объяснение: