Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
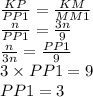
ответ: 3 см
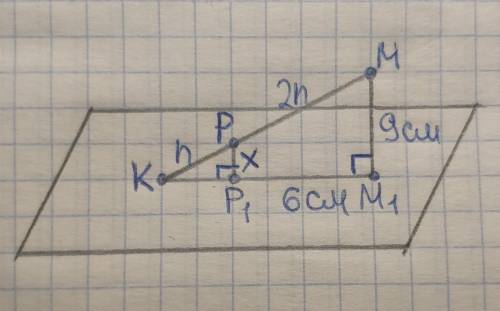
a*b=48 a=48/b
a²+b²=10² (48/b)²+b²=100⇒2304/b²+b²=100⇒2304+b⁴=100b²
b⁴-100b²+2304=0
b²=x; x²-100x+2304=0
D=784
x=64⇒ b²=64⇒b=8⇒a=6
x=36⇒b²=36⇒b=6⇒a=8
6 и 8 стороны прямоугольника⇒ Р=(6+8)*2=28
ответ: 28.