Столбы ставят перпендикулярно земле, а, следовательно, они параллельны между собой. Таким образом, получим, что ситуация, описанная в задаче, представляет собой следующую задачу:
Дана прямоугольная трапеция АВСD, основания которой BC = 9м и AD = 15м, а боковая сторона СD = 16м. Найдем сторону АВ (см. рис.).
Проведем СМ ⊥ AD, тогда ВС = АМ и АВ = СМ.
Получим прямоугольный треугольник СМD, у которого гипотенуза СD = 16 м, МD = АD - АМ = АD - ВС = 15- 9 = 6 (м).
По теореме Пифагора СМ² = СD² - МD² = 16² - 6² = 256 - 36 = 220 =
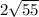
, откуда СМ =
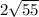
м.
Значит. и АВ =
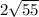
м.
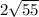
м
∠А+∠В+∠С=180°
3х+7х+90°=180°
10х=90°
х=9°
∠А=3*9°=27°
∠В=7*9°=63°
5. Нехай ∠А=х, тоді ∠В=х+37°
∠А+∠В+∠С=180°
х+х+37°+90°=180°
2х=53°
х=26,5°
∠А=26,5°
∠В=26,5°+37°=63,5°