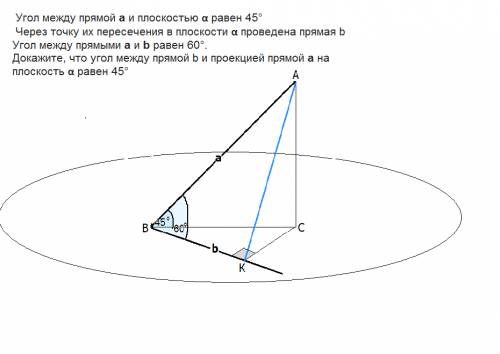
Обозначим начало наклонной А, конец наклонной В ( точка пересечения с плоскостью α).
Опустим из А перпендикуляр на плоскость α.
ВС- проекция наклонной а.
АС⊥ВС.
Угол АВС=45°
Прямую b обозначим ВК; угол АВК=60°
Рассмотрим треугольник АВС.
Так как угол АВС=45°, то угол ВАС=45°,
треугольник АВС прямоугольный равнобедренный.
АС=ВС=а*sin(45°)=(a√2):2.
Треугольник АВК прямоугольный.
ВК=а*cos(60°)=а:2
Треугольник ВКС - прямоугольный с гипотенузой ВС
cos ∠ KBC=BК:ВС=(а:2):(a√2):2=1:√2. Умножив числитель и знаменатель на √2, получим
cos ∠ KBC=√2):2. Это косинус 45°
(х-10) см - вторая сторона;
(х+10) см - третья сторона;
(2(х-10)=2х-20) см - четвертая сторона.
х+х-10+х+10+2х-20=80.
5х=100;
х=20 см.
Тогда другие стороны:
20-10=10см - вторая сторона
20+10=30см - третья сторона
2*10=20см - четвертая сторона
ответ: 20см - первая сторона
10см - вторая сторона
30см - третья сторона
20см - четвертая сторона